Resolución de sudokus (7)
XY-Wing.
XY Wing
La idea de este método es sencilla, aunque localizar dónde aplicarla en un sudoku puede que no sea tan intuitivo.
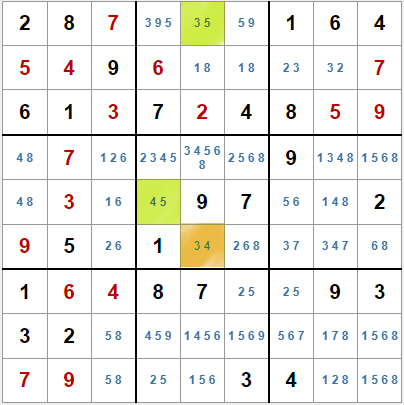
Se trata de localizar tres casillas con dos candidatos cada una que formen un trio, es decir, que tengan tres candidatos entre las tres. Una de las casillas a la que llamaremos 'pivote' estará en la misma zona (fila, columna o caja) que cada una de las otras casillas, a las que llamaremos 'alas'.
En nuestro ejemplo, la casilla en naranja es nuestro pivote. Está en la misma caja que la casilla en E4, el ala izquierda y en la misma columna que la casilla A5, el ala derecha. Además forma el trío de valores [3, 4, 5]. El pivote además, comparte uno de los valores con cada ala, el 4 con la izquierda y en 3 con la derecha.
Nos fijamos ahora en el valor común entre las dos alas, en este caso el 5. Podremos eliminar el valor 5 de las casillas que compartan zona con las dos alas. Es decir, la A4 y la D5. Si la casilla E5 tuviera como candidato el 5 también se podría eliminar.
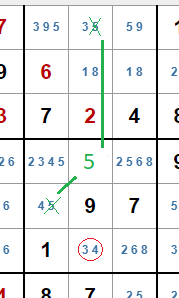
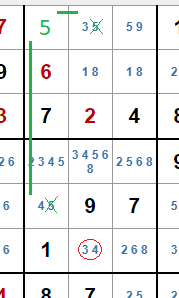
Verificar esto es sencillo. Imaginemos que colocamos un 5 en la casilla A4. Esto implica que en la casilla A5 debe haber un 3 y en la casilla E4 un 4. Eso no deja ningún valor posible para el pivote, ya que comparte caja con la casilla E4, lo que elimina el candidato 4 y comparte columna con la casilla A5, lo que elimina el candidato 3.
Si colocamos un 5 en la casilla D5 implica un 3 en la casilla A5 y un 4 en la casilla E4, con el mismo resultado para el pivote.
El problema ahora es localizar casillas en las que se pueda aplicar esta técnica.
Lo primero será buscar casillas con dos candidatos.
Sabemos que para tener un patrón XY-Wing una casilla debe compartir grupo con las otras dos. Hay tres casos:
- El pivote comparte fila con un ala y columna con la otra.
- El pivote comparte fila con un ala y caja con la otra.
- El pivote comparte columna con un ala y caja con la otra.
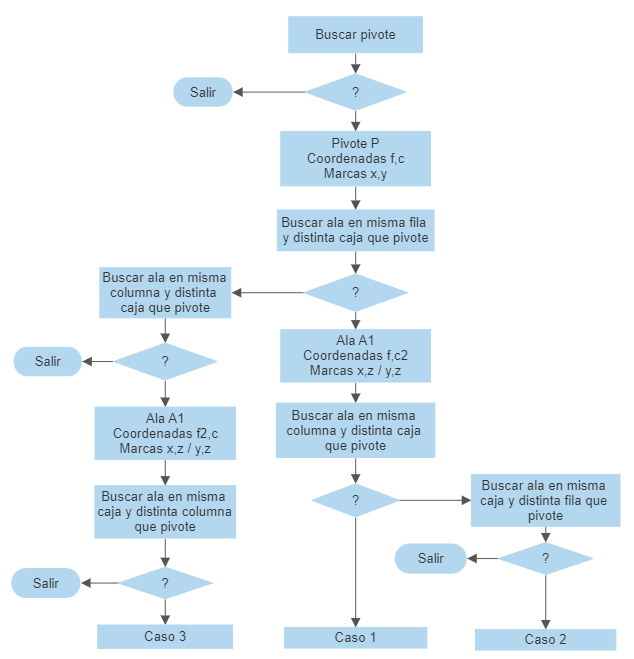
Nuestro algoritmo comienza por buscar un candidato a pivote, esto es, una casilla con dos marcas de lápiz. Si la encuentra, buscará un ala en la misma fila, fuera de la caja en la que está el pivote, con dos marcas de lápiz, y una de ellas compartida con el pivote.
Si encuentra esa primera ala, buscará la segunda en la misma columna y diferente caja que el pivote. También es una casilla con dos marcas de lápiz, aunque en este caso una de ellas la compartirá con el pivote y la otra con la primera ala.
Si esa casilla existe, estaremos en el caso 1.
Si no es así, buscaremos una casilla con las mismas características, pero en la misma caja y distinta fila que el pivote. Si esa casilla existe, estaremos en el caso 2.
Si no hemos encontrado el ala 1 en la misma fila que el pivote, la buscaremos en la misma columna y diferente caja.
Si la encontramos, buscaremos la segunda ala en la misma caja y distinta columna que el pivote. Si encontramos las dos, estaremos en el caso 3.
Hay que tener en cuenta algunos detalles:
Al buscar la primera ala se puede dar el caso de que haya dos posibles candidatos. Si por ejemplo, el pivote tiene los candidatos x, y, puede haber dos casillas en la misma fila o columna con los candidatos x,z o y, z.
Esto no pasa con la segunda ala, ya que sus marcas de lápiz quedarán determinadas a partir de las marcas de lápiz del pivote y la primera ala. Por ejemplo, si el pivote tiene las marcas x, y y la primera ala x,z, la segunda ala debe tener obligatoriamente las marcas y, z.
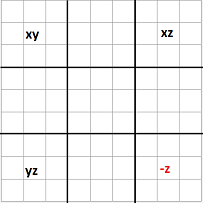
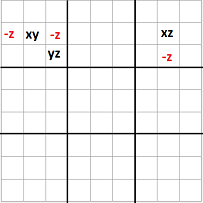
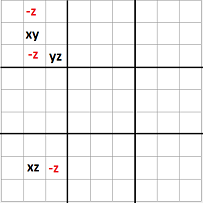
En principio puede parecer que hay otros dos posibles casos. En el caso 2, que la segunda ala esté en la caja de la derecha y en el caso 3 , que la segunda ala esté en la caja de abajo. Sin embargo esos casos son similares en cuanto al algoritmo se refiere.
En las imágenes de la izquierda se muestran las casillas que pueden verse afectadas en cada caso, en las que se puede eliminar, si está presente, el candidato común a ambas alas.
Necesitaremos algunos métodos nuevos en la clase tablero:
class Tablero {
private:
...
bool ProcesarXYWingCaso1(Casilla *pivote, Casilla *ala1, Casilla *ala2);
bool ProcesarXYWingCaso2(Casilla *pivote, Casilla *ala1, Casilla *ala2);
bool ProcesarXYWingCaso3(Casilla *pivote, Casilla *ala1, Casilla *ala2);
...
public:
...
bool ProcesaXYWing();
...
};
Por ejemplo, para buscar patrones XY-Wing trasladaremos nuestro algoritmo:
bool Tablero::ProcesaXYWing() {
int f, c;
Casilla *pivote;
Casilla *ala1;
Casilla *ala2;
int c1, f1;
for(f=0; f<9; f++) {
for(c=0; c<9; c++) {
if(casilla[f][c].Lapiz().CuentaMarcas() == 2) { // Posible pivote
pivote = &casilla[f][c];
c1 = 0;
do {
ala1 = fila[f].BuscaAla1MenosCaja(pivote, c1);
if(ala1) { // Tenemos posible ala 1 en f,c2 Casos 1/2
c1 = ala1->Columna()+1; // Probar si hay más candidatos a ala1
// Buscar ala2
ala2 = columna[c].BuscaAla2MenosCaja(pivote, ala1);
if(ala2) { // Patrón XY-Wing caso 1
if(ProcesarXYWingCaso1(pivote, ala1, ala2)) return true;
} else { // Posible caso 2
ala2 = caja[pivote->Caja()].BuscaAla2MenosFila(pivote, ala1);
if(ala2) { // Patrón XY-Wing caso 2
if(ProcesarXYWingCaso2(pivote, ala1, ala2)) return true;
}
}
} else { // Posible caso 3
c1 = 9; // No hemos encontrado el ala1 en la fila f. No seguir buscando.
f1 = 0;
do {
ala1 = columna[c].BuscaAla1MenosCaja(pivote, f1);
if(ala1) { // Tenemos posible ala 1 en f2,c
f1 = ala1->Fila()+1;
ala2 = caja[pivote->Caja()].BuscaAla2MenosColumna(pivote, ala1);
if(ala2) { // Patrón XY-Wing caso 3
if(ProcesarXYWingCaso3(pivote, ala1, ala2)) return true;
}
}
} while(ala1 && f1 < 9); // Probar si hay más candidatos a ala1
}
} while(ala1 && c1 < 9);
}
}
}
return false;
}
Necesitamos añadir algunos métodos a las clases Fila, Columna y Caja que nos ayuden a localizar alas.
Para la clase Fila solo añadiremos una función:
class Fila {
...
public:
...
Casilla *BuscaAla1MenosCaja(Casilla *pivote, int c1=0);
};
La implementación no es muy complicada:
Casilla *Fila::BuscaAla1MenosCaja(Casilla *pivote, int c1) {
int k = pivote->Caja();
for(int c=c1; c<9; c++) {
// Distinta caja con dos marcas de lápiz
if(cas[c]->Caja() != k && cas[c]->Lapiz().CuentaMarcas() == 2) {
// La casilla tiene un candidato en común con el pivote
if((cas[c]->Lapiz() + pivote->Lapiz()).CuentaMarcas() == 3) {
return cas[c];
}
}
}
return NULL;
}
Para la clase Columna añadiremos dos funciones:
class Columna {
...
public:
...
Casilla *BuscaAla1MenosCaja(Casilla *pivote, int f1=0);
Casilla *BuscaAla2MenosCaja(Casilla *pivote, Casilla *ala1);
};
La primera es análoga a la de la clase Fila. La segunda es algo diferente:
Casilla *Columna::BuscaAla2MenosCaja(Casilla *pivote, Casilla *ala1) {
int k = pivote->Caja();
MarcasLapiz nocomunes = (pivote->Lapiz() + ala1->Lapiz()) - (pivote->Lapiz() ^ ala1->Lapiz());
for(int f=0; f<9; f++) {
// Distinta caja con las dos marcas de lápiz comunes
if(cas[f]->Caja() != k && cas[f]->Lapiz() == nocomunes) {
return cas[f];
}
}
return NULL;
}
Finalmente, para la clase Caja, también dos funciones:
class Caja {
...
public:
...
Casilla *BuscaAla2MenosFila(Casilla *pivote, Casilla *ala1);
Casilla *BuscaAla2MenosColumna(Casilla *pivote, Casilla *ala1);
};
Son dos funciones similares, una para filas y otra para columnas:
Casilla *Caja::BuscaAla2MenosFila(Casilla *pivote, Casilla *ala1) {
int f = pivote->Fila();
MarcasLapiz nocomunes = (pivote->Lapiz() + ala1->Lapiz()) - (pivote->Lapiz() ^ ala1->Lapiz());
for(int p=0; p<9; p++) {
// Distinta Fila con las dos marcas de lápiz comunes
if(cas[p]->Fila() != f && cas[p]->Lapiz() == nocomunes) {
return cas[p];
}
}
return NULL;
}
Por último, nos faltan las funciones para procesar los patrones XY-Wing que detectemos:
bool Tablero::ProcesarXYWingCaso1(Casilla *pivote, Casilla *ala1, Casilla *ala2) {
MarcasLapiz comun = ala1->Lapiz() ^ ala2->Lapiz();
int valor = comun.Valor();
if(casilla[ala2->Fila()][ala1->Columna()].Lapiz().EliminaMarca(valor)) return true;
return false;
}
bool Tablero::ProcesarXYWingCaso2(Casilla *pivote, Casilla *ala1, Casilla *ala2) {
bool retval = false;
MarcasLapiz comun = ala1->Lapiz() ^ ala2->Lapiz();
int valor = comun.Valor();
int c1, c2, c3;
int k = pivote->Caja();
c1 = caja[k].Cas(0)->Columna();
c2 = caja[k].Cas(1)->Columna();
c3 = caja[k].Cas(2)->Columna();
retval = casilla[ala2->Fila()][ala1->Columna()].Lapiz().EliminaMarca(valor);
retval |= casilla[pivote->Fila()][c1].Lapiz().EliminaMarca(valor);
retval |= casilla[pivote->Fila()][c2].Lapiz().EliminaMarca(valor);
retval |= casilla[pivote->Fila()][c3].Lapiz().EliminaMarca(valor);
return retval;
}
bool Tablero::ProcesarXYWingCaso3(Casilla *pivote, Casilla *ala1, Casilla *ala2) {
bool retval = false;
MarcasLapiz comun = ala1->Lapiz() ^ ala2->Lapiz();
int valor = comun.Valor();
int f1, f2, f3;
int k = pivote->Caja();
f1 = caja[k].Cas(0)->Fila();
f2 = caja[k].Cas(3)->Fila();
f3 = caja[k].Cas(6)->Fila();
retval = casilla[ala1->Fila()][ala2->Columna()].Lapiz().EliminaMarca(valor);
retval |= casilla[f1][pivote->Columna()].Lapiz().EliminaMarca(valor));
retval |= casilla[f2][pivote->Columna()].Lapiz().EliminaMarca(valor));
retval |= casilla[f3][pivote->Columna()].Lapiz().EliminaMarca(valor));
return false;
}
En la versión del programa para descargar estas tres funciones son algo más complicadas, ya que generan un fichero con las instrucciones para solucionar el sudoku.
Bucle de resolución
En nuestra función main, en el bucle de resolución de la fase 2, invocaremos a cada método de este modo:
do {
...
if(!repetir && T.ProcesaXYWing()) {
repetir = true;
T.VerificarFinales();
}
} while(repetir);
| Nombre | Fichero | Fecha | Tamaño | Contador | Descarga |
|---|---|---|---|---|---|
| Sudoku7 | sudoku7.zip | 2022-06-22 | 23232 bytes | 786 |