Resolución de sudokus (17)
Más patrones de solución única
No he encontrado ésta técnica documentada en ningún sitio, aunque estoy bastante seguro de que es válida..
Patrón de solución única tipo C
Se trata de una extensión del patrón de solución única que vimos en Sudoku10.

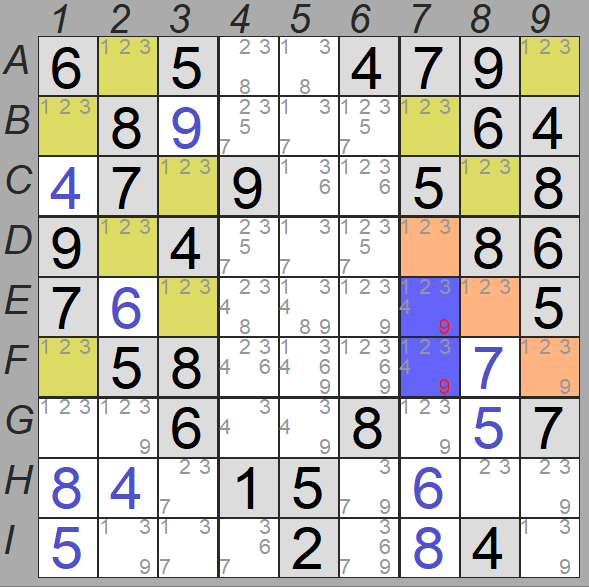
Veamos el sudoku del ejemplo de la derecha. En amarillo hay resaltadas seis casillas con los candidatos 2 y 4, salvo C4, que además contiene el 6 como candidato.
Si eliminamos el 6 como candidato en C4, el sudoku tendrá dos potenciales soluciones, y un sudoku bien formado solo puede tener una solución, por lo tanto, podemos eliminar los dos candidatos, 2 y 4, o asignar el valor 6 en la casilla C4.
En un caso más general, el candidato extra puede estar en las dos casillas de la caja. En ese caso sabemos que ese valor debe estar en una de esas dos casillas, así que podríamos eliminar ese candidato extra del resto de la caja y de la fila o columna donde estén esas casillas.
En este sudoku hay otro patrón similar, formado por las casillas H2, I2, H7, I7, B7 y B8. En este caso los candidatos comunes son 1 y 2, salvo en B8, que también contiene el 3. Lo mismo pasa con el patrón anterior, en la casilla B8 podemos eliminar los candidatos 1 y 2.
Este sudoku en particular contiene dos patrones de este tipo, pero aunque no vayamos a encontrar muchos sudokus con estos patrones, cuando lo hagamos serán de gran ayuda. Así que vale la pena detectarlos ya que, al menos en este caso, ninguno de los métodos que hemos visto anteriormente consigue eliminar candidatos.
Tipos de patrones
Encontrar estos patrones puede que no parezca complicado, pero aunque sólo existen unas pocas variantes y visualmente, una vez destacadas las casillas, son evidentes, codificar el algoritmo no es trivial.
De hecho, el patrón es muy parecido al del pez espada. La diferencia es que ahora en cada casilla deben coincidir dos candidatos en lugar de uno. Por fuerza debe ser un patrón incompleto, ya que en cada dos filas o columnas sólo habrá dos casillas, puesto que cuatro de las casillas están ocupadas por pares desnudos.
Lo que todos los patrones tendrán en común es que dos de los pares desnudos ocuparán siempre dos casillas de la misma caja. Este será nuestro punto de partida para detectar patrones.
A priori existen tres variantes principales del patrón, con varias subvariantes en cada una, dependiendo de en qué casilla o casillas esté el candidato extra o la posición que ocupe la fila o columna con el par desnudo: encima, debajo, a derecha o izquierda.
Patrón A Patrón A' Patrón A"
abc ab ab abc abc abc
ab ab ab ab ab ab
ab ab ab ab ab ab
Patrón B Patrón B' Patrón B"
ab ab ab ab ab ab
ab abc ab ab ab abc
ab ab ab abc ab abc
Patrón C Patrón C' Patrón C"
ab ab ab ab ab ab
abc ab ab ab abc ab
ab ab abc ab abc ab
En la práctica, podemos considerar todos los patrones como equivalentes, ya que si intercambiamos filas y columnas podemos obtener el resto de patrones. Por ejemplo, si en el patrón A intercambiamos las posiciones de las filas primera y segunda, obtendremos el patrón B. Si intercambiamos las posiciones de las columnas primera y segunda, obtendremos el patrón A", con la pareja de candidatos diagonales invertidas, etc.
Algoritmo
Nuestro objetivo es encontrar las tres filas y columnas que contienen las casillas que forman el patrón, f1, f2, f3 y c1, c2, c3. Y el valor de los candidatos a y b.
- Recorreremos la lista de pares desnudos.
- Si el par "p1" desnudo está en la misma caja y columna.
- Almacenamos el valor de la columna en c3, las filas en f1 y f2 y los candidatos en v1 y v2.
- Recorremos de nuevo la lista de pares desnudos.
- Si el par "p2" es distinto del anterior "p1", está en la misma caja, pero no en la misma columna y contiene los candidatos v1 y v2.
- Si 'p2' está en la misma fila, tenemos un posible patrón C. *
- Almacenamos el valor de la fila en f3 y las columnas en c1 y c2.
- Si las casillas en (f1,c1)-(f2,c2) contienen los candidatos v1 y v2, y tienen 2 o 3 candidatos.
- Si solo una tiene tres candidatos, el tercero es v3 y procesamos el patrón.
- Si las dos tienen tres candidatos, y el tercero es el mismo en ambas, es v3 y procesamos el patrón.
- Si las casillas en (f1,c2)-(f2,c1) contienen los candidatos v1 y v2, y tienen 2 o 3 candidatos.
- Si solo una tiene tres candidatos, el tercero es v3 y procesamos el patrón.
- Si las dos tienen tres candidatos, y el tercero es el mismo en ambas, es v3 y procesamos el patrón.
- Si 'p2' está en la misma caja, se trata de una par desnudo en distintas filas y columnas. Posible caso A.
- Almacenamos las columnas de las casillas en c1 y c2.
- Buscamos en todas las filas, menos en f1 y f2 una en que las casillas (f1,c1)-(f2,c2) contengan los candidatos v1 y v2,
y tengan 2 o 3 candidatos. Si aparece, almacenamos c3.
- Si solo una tiene tres candidatos, el tercero es v3 y procesamos el patrón.
- Si las dos tienen tres candidatos, y el tercero es el mismo en ambas, es v3 y procesamos el patrón.
- Si el par "p1" desnudo está en la misma caja y fila.
- Almacenamos el valor de la columna en f3, las filas en c1 y c2 y los candidatos en v1 y v2.
- Recorremos de nuevo la lista de pares desnudos.
- Si el par "p2" es distinto del anterior "p1", está en la misma caja y contiene los candidatos v1 y v2.
- Si 'p2' está en la misma columna, tenemos un posible patrón C. El proceso es similar a *
- Si 'p2' está en la misma caja, pero no en la misma fila o columna estamos antes un posible caso B.
- Almacenamos las filas de las casillas en f1 y f2.
- Buscamos en todas las columna, menos en c1 y c2 una en que las casillas (f1,c1)-(f2,c2) contengan los candidatos v1 y v2,
y tengan 2 o 3 candidatos, si aparece, almacenamos f3.
- Si solo una tiene tres candidatos, el tercero es v3 y procesamos el patrón.
- Si las dos tienen tres candidatos, y el tercero es el mismo en ambas, es v3 y procesamos el patrón.
Procesar patrones
A la hora de procesar el patrón detectado hay que distinguir si hay una o dos casillas con el candidato extra.
Si hay dos casillas con el candidato extra:
En al caso del patrón A, deberemos eliminar como candidato el valor c de la fila y la caja donde estén esas casillas, f3.
En el caso del patrón B, deberemos eliminar como candidato el valor c de la columna y la caja donde estén esas casillas, c3.
En el caso del patrón C, deberemos eliminar como candidato el valor c únicamente de la caja donde estén esas casillas.
Si sólo hay una casilla con el candidato extra, para cualquiera de los tres patrones, deberemos eliminar como candidato el valor c en todas las casillas de la fila, columna y caja donde esté esa casilla, salvo en esa casilla. O lo que es lo mismo, podemos asignar el valor c a esa casilla.
He probado miles de sudokus diferentes, y sólo he encontrado uno al que puedo aplicar este método, aunque es posible que los candidatos que se podrían eliminar usándolo se hayan eliminado mediante cualquiera de los métodos anteriores. Evidentemente, este tipo de métodos de eliminación, cuanto más sofisticados son, menos posibilidades de aplicarlos encontraremos.
Patrones de solución única tipo D
Aún existe otro patrón de solución única más elaborado, si es que eso es posible.
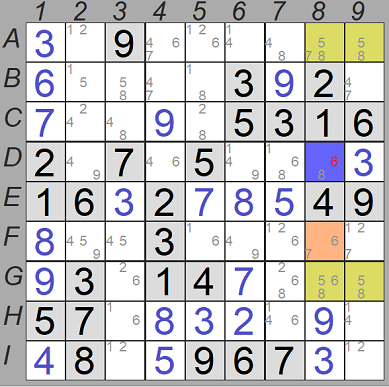
Se trata del patrón de la imagen de la derecha. En este caso se trata de un patrón compuesto por tríos desnudos. Podemos ver que existen tres cajas, 1, 3 y 4, en el que el trio de candidatos 1, 2 y 3 aparece en filas y columnas diferentes, de tal modo que cada casilla con el trio de candidatos aparece sólo en dos filas o columnas de esas tres cajas:
- En la fila A en las columnas 2 y 9.
- En la fila B en las columnas 1 y 7.
- En la fila C en las columnas 3 y 8.
- En la columna 1 en las filas B y F. (De momento ignoraremos la casillas G1, que no forma parte del grupo de cajas.)
- En la columna 2 en las filas A y D.
- En la columna 3 en las filas C y E.
Ahora fijaremos nuestra atención en la caja 6, que contiene ese mismo trio de candidatos en las casillas D7 y E8, y además, en la casilla F9 tenemos los mismos candidatos, 1, 2 y 3, además del 9.
De nuevo, podemos agrupar las casillas por parejas:
- En la fila D en las columnas 2 y 7.
- En la fila E en las columnas 3 y 8.
- En la fila F en las columnas 1 y 9.
- En la columna 7 en las filas B y D.
- En la columna 8 en las filas C y E.
- En la columna 9 en las filas A y F.
Al igual que en los patrones de solución única que hemos visto anteriormente, si el candidato extra sólo aparece en una de las casillas, podemos asignar ese valor a esa casilla, o lo que es lo mismo, eliminar ese candidato del resto de la fila, columna y caja donde esté esa casilla.
Si el candidato extra apareciese en dos o las tres casillas de una caja, sólo podríamos eliminar ese candidato del resto de casillas de esa caja.
De nuevo nos encontramos con un patrón que es más fácil de ver que de detectar mediante un programa. Si el método para buscar patrones de tipo C era largo, el de patrones de tipo D promete ser una pesadilla. Pero, hemos venido a jugar.
El patrón básico tiene esta forma:
c1 c2 c3 c4 c5 c6 f1 abc --- --- abc --- --- f2 --- abc --- --- abc --- f3 --- --- abc --- --- abc f4 abc --- --- abcd --- --- f5 --- abc --- --- abcd-- --- f6 --- --- abc --- --- abcd
En este patrón podemos intercambiar el orden de las filas f1, f2 y f3, y el de las filas f4, f5 y f6, así como el de las columnas c1, c2 y c3 y el de las columnas c4, c5 y c6. Por ejemplo, intercambiando f5 y f6 y c2 y c3 tendremos el patrón:
c1 c3 c2 c4 c5 c6 f1 abc --- --- abc --- --- f2 --- --- abc --- abc --- f3 --- abc --- --- --- abc f4 abc --- --- abcd --- --- f6 --- abc --- --- --- abcd f5 --- --- abc --- abcd-- ---
Por supuesto, el candidato extra d puede aparecer en una, dos o las tres casillas de la caja.
Algoritmo
Creo que lo más lógico sería empezar buscando tres cajas con tres casillas que tengan el mismo trio desnudo. Además, esas tres cajas deben tener una fila y columna de cajas en común, es decir, o bien dos de las cajas deben estar en la misma fila de cajas y dos cajas en la misma columna de cajas.
Después debemos verificar si las casillas en la misma fila de cajas tienen dos casillas con los candidatos en cada fila, y si las casillas en la misma columna de cajas tiene dos casillas en cada columna.
Para completar el patrón nos olvidamos de la caja que comparte fila y columna con las otras dos, y buscamos en las intersecciones de esas cajas las casillas que completan el patrón.
Este algoritmo sirve para localizar patrones tanto para un jugador humano como para un programa, pero nuestro programa también almacena tríos desnudos, de modo que es posible que podamos simplificar algo la versión de software.
- Para cada caja, empezaremos localizando una casilla con tres candidatos en la primera fila.
- Si la encontramos, buscamos una casilla en la segunda fila de la caja con los mismos candidatos, pero en distinta columna.
- Si la encontramos, verificamos si en la tercera fila y en la columna restante tenemos una casilla con los mismos candidatos.
- En ese caso, tenemos la caja k1.
- Ahora buscamos casillas con los mismos candidatos y las mismas condiciones en las dos cajas de la misma fila de cajas que k1.
- Si localizamos esa caja, tenemos la caja k2.
- Ahora buscamos casillas con los mismos candidatos y las mismas condiciones en las dos cajas de la misma columna que k1.
- Si encontramos esa caja, tenemos la caja k3.
- La caja k4 estará en la misma columna de cajas que k2 y en la misma fila de cajas que k3.
- Buscamos ahora en la caja k4 tres casillas, en filas y columnas diferentes que contengan los mismos candidatos, o uno más, siempre que sea el mismo.
- Si la caja k4 cumple todas las condiciones, podemos eliminar el candidato extra del resto de la caja.

Patrón de solución única tipo E
Empiezo a pensar que nos quedaremos sin letras para este tipo de patrones.
Volvemos a patrones de solución única de cuatro casillas. En el sudoku de la derecha tenemos uno de esos patrones formado por las casillas B1, B2, F1 y F2. En este patrón partimos de dos casillas con dos candidatos, un par desnudo. Si las dos casillas están en la misma fila, y en la misma caja, tendremos que buscar otras dos casillas en otra fila y en las mismas columnas, si están en la misma columna, las buscaremos en otra columna en las mismas filas.
Estas dos casillas deben incluir los mismos candidatos, entre otros. Los candidatos extra no son relevantes, salvo porque deben existir. Además, esas dos casillas tienen que cumplir que uno de los candidatos sólo aparezca en esas dos casillas de su misma fila o columna.
En este ejemplo, las casillas B1 y B2 tienen los candidatos 1 y 6, y las casillas que completan el patrón, F1 con los candidatos 1, 4, 5 y 6 y F2, con los candidatos 1, 6 y 9. Además, en la fila F, el candidato 6 sólo aparece en las casillas F1 y F2.
En este caso podemos eliminar como candidatos el 1 en las casillas F1 y F2.
El razonamiento es el siguiente:
Si en B1 hay un 6, en F2 debe haber un 6 y en B2 debe haber un 1. Si en F1 hubiese un 1 tendríamos un patrón prohibido.
El mismo razonamiento se puede aplicar si consideramos que F2 contiene un 6, eliminando el 1 como candidato en F2.

Existe una variante en la que las casillas del par desnudo ocupan cajas diferentes. En este caso, las casillas con los candidatos extra deben estar en las mismas cajas que las casillas con el par desnudo.
Será necesario modificar los métodos para buscar pares desnudos: ProcesaParesDesnudosFila y ProcesaParesDesnudosColumna, para que consideren también los casos en los que las dos casillas del par desnudo ocupen cajas diferentes de la misma fila o columna.
Algoritmo
- Recorremos la lista de pares desnudos.
- Si las dos casillas del par desnudo están en la misma caja.
- Si están en la misma fila.
- Buscamos en el resto de filas dos casillas en las mismas columnas que:
contengan más de dos candidatos y
que dos de ellos sean los mismos que los del par desnudo.
- Si uno de los candidatos sólo aparece en esas dos casillas de la fila, eliminamos el otro valor como candidato.
- Si están en la misma columna.
-Buscamos en el resto de columnas dos casillas en las mismas filas que:
contengan más de dos candidatos y
que dos de ellos sean los mismos que los del par desnudo.
- Si uno de los candidatos sólo aparece en esas dos casillas de la columna, eliminamos el otro valor como candidato.
- Si no están en la misma caja.
- Si están en la misma fila.
- Buscamos en la misma fila de cajas dos casillas en las mismas columnas que:
contengan más de dos candidatos y
que dos de ellos sean los mismos que los del par desnudo.
- Si uno de los candidatos sólo aparece en esas dos casillas de la fila, eliminamos el otro valor como candidato.
- Si están en la misma columna.
- Buscamos en la misma columna de cajas dos casillas en las mismas filas que:
contengan más de dos candidatos y
que dos de ellos sean los mismos que los del par desnudo.
- Si uno de los candidatos sólo aparece en esas dos casillas de la columna, eliminamos el otro valor como candidato.

Variantes del patrón de solución única tipo B
Como ha pasado con otros patrones, el patrón de solución única de tipo B que vimos en sudoku 10 está incompleto.
Recordemos que el patrón estaba formado por cuatro casillas que ocupaban dos cajas. Dos de las casillas tenían la misma pareja de candidatos, y las otras dos tenían además un tercer candidato.
Como sucede con el patrón de tipo E, existe una variante en la que las dos casillas que forman el par desnudo no estén en la misma caja. Este es el caso del sudoku de la derecha. Partimos del par desnudo formado por A2 y A4, con los candidatos 2 y 4, cuyas casillas están en cajas diferentes, a 1 y la 2. Para completar el patrón tenemos que encontrar otras dos casillas, en las cajas 1 y 2, en las mismas columnas 2 y 4, con los mismos candidatos, 2 y 4, y un candidato extra, en este caso el 6. Las casillas C2 y C4 tenemos un patrón de tipo B'. Ahora podremos eliminar el candidato extra de la fila C.
El mismo patrón se puede formar partiendo de un par desnudo en una columna.

Patrón de solución única tipo F
Pero, aún existen más patrones de solución única.
Veamos el sudoku de la izquierda formado por las casillas E4, E6, B4 y B6. Es parecido al tipo B, pero en este caso, el candidato extra no es el mismo en las dos casillas B4 y B6. Ahora tenemos que buscar en la zona que comparten esas casillas, en la fila B y en la caja 2, otra casilla que tenga únicamente esos dos candidatos extra, el 6 y el 9.
En este ejemplo esa casilla es la B5, que comparte caja y fila con B4 y B6.
Ahora analicemos el patrón. Siguiendo el mismo razonamiento que en otros patrones de solución única, podemos afirmar que o bien en la casilla B4 hay un 9, o que en B6 hay un 6. No pueden darse los dos casos, ya que la casilla B5 se quedaría sin candidatos.
En el primer caso, si en B4 hay un 9 en B5 debe haber un 6. Esto elimina como candidatos el 6 y el 9 en el resto de la caja y la fila.
En el segundo caso, si en B6 hay un 6 en B5 debe haber un 9. De nuevo, esto elimina como candidatos el 6 y el 9 en el resto de la caja y la fila.
Si la casilla con los dos candidatos estuviese en en la misma caja que B4 y B6, pero en otra fila, sólo podríamos eliminar los candidatos del resto de la caja 2. Del mismo modo, si la casilla con los dos candidatos estuviese en una casilla de la fila B en las cajas 1 ó 3, sólo podríamos eliminar los candidatos del resto de la fila B.
El mismo razonamiento es aplicable sustituyendo filas por columnas.
Como en el caso del patron E, en este también existe una variante en la que las casillas del par desnudo ocupan cajas diferentes. En este caso, las casillas con los candidatos extra deben estar en las mismas cajas que las casillas con el par desnudo y sólo se podrían eliminar candidatos en la fila o columna en la que estén las casillas con los candidatos extra.
Algoritmo
El algoritmo es parecido al del patrón de tipo E.
Podríamos pensar que hay que tener cuidado de verificar que los dos candidatos extra son diferentes, ya que si fuesen iguales estaríamos ante un patrón tipo B, que tiene un tratamiento diferente.
En realidad no es necesario, ya que en ese caso la casilla que completa el patrón F, y que debe tener los dos candidatos, sólo tendría uno, y por lo tanto sería un valor final. Pero sabemos que no puede haber una casilla con ese valor final, ya que está como candidato en la caja, fila o columna.
- Recorremos la lista de pares desnudos.
- Si las dos casillas del par desnudo están en la misma caja.
- Si están en la misma fila.
- Buscamos en el resto de filas dos casillas en las mismas columnas que:
contengan tres candidatos y
que dos de ellos sean los mismos que los del par desnudo.
- Buscamos casillas en la caja y fila con esos dos candidatos.
- Si existe alguna procesamos el patrón.
- Si están en la misma columna.
-Buscamos en el resto de columnas dos casillas en las mismas filas que:
contengan tres candidatos y
que dos de ellos sean los mismos que los del par desnudo.
- Buscamos casillas en la caja y columna con esos dos candidatos.
- Si existe alguna procesamos el patrón.
- Si no están en la misma caja.
- Si están en la misma fila.
- Buscamos en la misma fila de cajas dos casillas en las mismas columnas que:
contengan tres candidatos y
que dos de ellos sean los mismos que los del par desnudo.
- Buscamos casillas en la fila con esos dos candidatos.
- Si existe alguna procesamos el patrón.
- Si están en la misma columna.
- Buscamos en la misma columna de cajas dos casillas en las mismas filas que:
contengan tres candidatos y
que dos de ellos sean los mismos que los del par desnudo.
- Buscamos casillas en la columna con esos dos candidatos.
- Si existe alguna procesamos el patrón.
| Nombre | Fichero | Fecha | Tamaño | Contador | Descarga |
|---|---|---|---|---|---|
| Sudoku 22 | sudoku22.zip | 2025-06-17 | 50531 bytes | 539 |