Resolución de sudokus (11)
XYZ-Wing.
XYZ-Wing
La idea de este método es relativamente sencilla, si comprendemos correctamente cómo funciona un patrón XY-Wing.
Si partimos de un patrón XY-WIng, y añadimos al pivote el candidato común de las dos alas, tenemos un patrón XYZ-Wing.
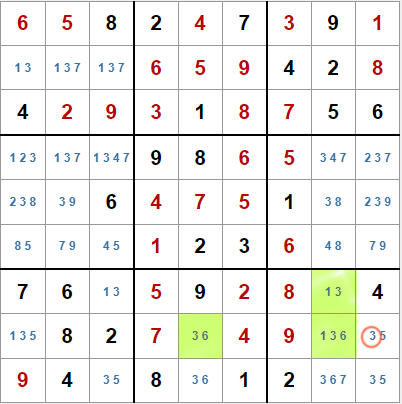
En el ejemplo de la derecha tenemos un patrón XYZ-Wing. En este caso, los valores XY son el 1 y el 6, y el 3 es Z. En un patrón XY-Wing el valor 3 del pivote no estaría presente. Este patrón nos permite eliminar el candidato 3 en la fila I, de la novena caja, excepto en el pivote. En este caso solo del casillero I9.
Esto es fácil de verificar. Si el valor 3 está en el ala I5, eso elimina el candidato 3 de la fila I. Si estuviera en G8, eliminaría el 3 como candidato en la caja 9, y si estuviese en el pivote, también. En cualquier caso, el candidato 3 no podría estar en I7 ni en I9.
Sin embargo, localizar estos patrones no es muy intuitivo. Partiremos de casillas con tres candidatos, e intentaremos buscar dos alas que cumplan el patrón XYZ-Wing.
Pongamos que nuestro candidato a pivote tiene los candidatos 'abc'. Tenemos que encontrar dos casillas que tengan cada una una zona en común con el pivote: fila, columna o caja, y que tengan una de las siguientes parejas de pares de valores:
- ab, ac
- ab, bc
- ac, ab
- ac, bc
- bc, ab
- bc, ac
Tal como pasaba con los patrones XY-Wing, las tres casillas no pueden compartir la misma zona. Es decir, no pueden estar en la misma fila, columna o caja, ya que en ese caso se trataría de trios desnudos.
Al contrario que con los patrones XY-Wing, en este caso tenemos dos ventajas:
- Sabemos que la casilla con tres candidatos es el pivote, por lo tanto la búsqueda de alas estará limitada a la fila, columna y caja en la que se encuentra la casilla con tres candidatos. Esto simplifica mucho la búsqueda de patrones.
- Solo se pueden eliminar candidatos en casillas visibles por las tres casillas que componen el patrón, por lo tanto, una de las alas debe estar, por fuerza, en la misma caja que el pivote.
De todos modos, nuestro algoritmo tiene que procesar muchas posibilidades para localizar un patrón XYZ-Wing
Empezaremos por buscar casillas con tres candidatos, y las tres posibles parejas de candidatos a partir de ellos.
A continuación buscaremos casillas en la fila, columna y caja en la que se encuentra nuestro pivote con esas posibles parejas de candidatos, y almacenaremos su columna, fila o posición, respectivamente, para cada pareja de candidatos localizada, o -1 si no existe tal casilla.
Estos valores se almacenarán en un array pos de 3x2, en la que el primer índice indica si se trata de casillas en filas, columnas o caja, y el segundo la pareja de candidatos que contiene.
Con estos datos ya podemos recorrer el índice 2, correspondiente a la caja. Recordemos que una de las parejas de candidatos debe estar en la misma caja que el pivote.
Para cada valor de pos[2] distinto de -1 buscaremos en pos[0] y pos[1] valores distintos de -1 y correspondientes a una pareja de candidatos distinta a la de la caja, es decir, con índices diferentes.
Para las clases Fila, Columna y Caja añadiremos un nuevo método BuscarMarcas, que buscará una casilla con las marcas de lápiz que pasaremos como parámetro:
class Fila {
private:
...
public:
...
int BuscarMarcas(const MarcasLapiz &m);
};
Se trata de una función sencilla:
// Devuelve la columna en la fila fil de la casilla con las marcas de lápiz m
// o -1 si no existe.
int Fila::BuscarMarcas(const MarcasLapiz &m) {
for(int c=0; c<9; c++) {
if(cas[c]->Lapiz() == m) return c;
}
return -1;
}
En la clase Tablero añadiremos un par de métodos privados y uno público:
class Tablero {
private:
...
bool ProcesarXYZFila(int k, int fil, int col, int v);
bool ProcesarXYZColumna(int k, int fil, int col, int v);
...
public:
...
bool ProcesaXYZWing();
...
};
Ambos son similares, uno para patrones con un ala detectada en la fila y otra para un ala detectada en la columna:
bool Tablero::ProcesarXYZFila(int k, int fil, int col, int v) {
bool retval=false;
// Hay que eliminar el candidato v en la fila fil de la caja k,
// excepto en la columna en que está el pivote.
for(int p=0; p<9; p++) {
if(caja[k].Cas(p)->Fila() == fil && caja[k].Cas(p)->Columna() != col)
retval |= caja[k].Cas(p)->Lapiz().EliminaMarca(v);
}
return retval;
}
Y el método para buscar y procesar patrones XYZ-Wing:
// Para cada casilla con tres candidatos buscamos dos alas compatibles con un patrón XYZ-Wing
bool Tablero::ProcesaXYZWing() {
MarcasLapiz m[3];
int i, j, k, v;
int pos[3][3]; // array con zonas, indice 1 (f, c, k) e indice 2 con las marcas,
for(int f=0; f<9; f++) {
for(int c=0; c<9; c++) {
if(casilla[f][c].Lapiz().CuentaMarcas() == 3) {
// Calcular las tres combinaciones de marcas de lápiz
// empezamos con las tres, y eliminamos una distinta en cada una
m[0] = m[1] = m[2] = casilla[f][c].Lapiz();
i=0;
for(int v=1; v<=9; v++) {
if(m[i].ContieneMarca(v)) { m[i++].EliminaMarca(v); }
}
k = casilla[f][c].Caja();
// Buscar en misma fila, columna y caja casillas con dos candidatos coincidentes
for(i = 0; i<3; i++) {
pos[0][i] = fila[f].BuscarMarcas(m[i]);
pos[1][i] = columna[c].BuscarMarcas(m[i]);
pos[2][i] = caja[k].BuscarMarcas(m[i]);
}
// Solo puede haber un patron XYZ-Wing si se ha detectado una casilla con marcas en la caja
for(i=0; i<3; i++) {
if(pos[2][i] != -1) { // Tenemos el par m[i] en la pos[2][i] de la caja
for(j=0; j<3; j++) { // Buscar las otras dos parejas en fila o columna
if(pos[0][j] != -1 && i!=j) { // Tenemos el par m[j] en la columna pos[0][j]
v = (m[i] ^ m[j]).Valor(); // Valor común de m[i] y m[j]
// Evitar trios desnudos, las tres casillas en la misma fila o caja
if(f!=caja[k].Cas(pos[2][i])->Fila() && casilla[f][pos[0][j]].Caja() != k)
if(ProcesarXYZFila(k, f, c, v)) return true;
}
if(pos[1][j] != -1 && i!=j) { // Tenemos el par m[j] en la fila pos[1][j]
v = (m[i] ^ m[j]).Valor(); // Valor común de m[i] y m[j]
// Evitar trios desnudos, las tres casillas en la misma columna o caja
if(c != caja[k].Cas(pos[2][i])->Columna() && casilla[pos[1][j]][c].Caja() != k)
if(ProcesarXYZColumna(k, f, c, v)) return true;
}
}
}
}
}
}
}
return false;
Bucle de resolución
Solo nos queda añadir este procedimiento al bucle:
do {
...
if(!repetir && T.ProcesaXYZWing()) {
repetir = true;
T.VerificarFinales();
}
} while(repetir);
| Nombre | Fichero | Fecha | Tamaño | Contador | Descarga |
|---|---|---|---|---|---|
| Sudoku14 | sudoku14.zip | 2022-06-22 | 30879 bytes | 669 |