Algoritmos
Partiremos de un laberinto que puede ser vacío y que el usuario podrá elegir en función de la dificultad, asignaremos a la serpiente una posición de salida y colocaremos comida en un punto del laberinto determinado.
Este será el único momento en el que la serpiente podrá estar parada, hasta que el usuario pulse una tecla.
A partir de ese momento, y a intervalos regulares de tiempo, que dependerán también del nivel de juego, se actualizará la posición de la serpiente. Windows nos permite crear programas multitarea, mediante el uso de hilos y de temporizadores. El avance de la serpiente será por lo tanto independiente de la velocidad con la que se ejecute el bucle del programa, y su velocidad de movimiento será constante.
Podemos crear un temporizador que actualice la posición, por ejemplo, cada 200 milisegundos, independientemente de lo que el usuario decida. Esto nos libera de la rigidez de los programas secuenciales, y nos permite ejecutar varias tareas simultaneasmente. En nuestro caso, el intervalo del temporizador dependerá del valor de velocidad elegido.
El algoritmo de actualización será más o menos este:
[Inicio]
<Serpiente en movimiento?>
Sí:
<Choque?>
Sí:
[Detener serpiente]
No:
<Es un objeto comestible?>
Sí:
[Incrementear unidades pendientes de crecer]
[Crear nuevo objeto comestible]
[Avanzar Serpiente]
[Salir]
Otra tarea que debemos atender es la encargada de leer el teclado y calcular la nueva dirección de movimiento.
Para ese cálculo debemos tener en cuenta que no es posible invertir la dirección de movimiento de la serpiente de golpe. Es decir, si la serpiente se mueve hacia arriba o hacia abajo, los movimientos posibles sólo serán hacia izquierda o derecha, o bien permanecer en la dirección actual. Lo mismo si la serpiente se mueve hacia la derecha o izquierda, los movimientos posibles serán arriba, abajo o permanecer en la dirección actual.
Esto nos obliga a tener dos variables para determinar el movimiento, una con el valor previo y otra con el próximo. Cada vez que se actualice la posición de la serpiente, copiaremos el valor actual en el previo, pero sólo si el valor actual es válido.
Según eso, podemos usar una variable para almacenar la última opción del usuario, que incluso puede cambiar varias veces entre movimiento y movimiento, de modo que sólo nos quedamos con la última opción.
Esto complica un poco la rutina de calcular la próxima posición de la cabeza, ya que se debe comprobar si la dirección deseada es legal o no.
Sin embargo, facilita el cálculo del tipo de sección que corresponde a la cabeza anterior, ya que disponemos de las direcciones anterior y actual.
Windows está orientado a eventos, y las pulsaciones de teclado generan mensajes de eventos de teclado. Concretamente nos interesa el mensaje WM_KEYDOWN, que se genera cada vez que se pulsa una tecla.
Procesar mensaje WM_KEYDOWN:
[Almacenar lectura en direccion deseada]
Calcular el valor de una sección
Hemos hablado algo más arriba de las secciones de la serpiente y de que pueden ser de varios tipos. Vamos a concretar algo más este tema.
Nuestra serpiente sólo puede desplazarse en cuatro direcciones, por lo tanto los giros siempre serán de noventa grados. Esto limita la secciones posibles a cuatro en ángulo, una vertical, una horizontal, cuatro posibles cabezas y cuatro colas. En total catorce secciones diferentes.
Veremos que los cálculos se simplifican mucho si optamos por codificar las direcciones y las secciones usando una lógica binaria. Por ejemplo, para cada dirección usamos un bit diferente, el primero para arriba, el segundo para la derecha, el tercero para abajo y el cuarto para la izquierda. Es decir, los valores serían 1, 2, 4 y 8, respectivamente.
O expresado en binario:
1: 0001 2: 0010 4: 0100 8: 1000
De este modo, para codificar una sección vertical usaremos los bits correspondientes a las direcciones arriba y abajo, es decir 1+4=5, para una sección horizontal los bits de las direcciones izquierda y derecha, 2+8=10.
1: 0001 4: 0100 5: 0101 2: 0010 8: 1000 10: 1010
Para el resto de las secciones haremos igual, la sección izquierda y abajo tendría el valor 4+8=12, etcétera. Cada sección curva tendrá un nombre dependiendo de la sección de circunferencia a que corresponda, la primera será de de izquierda-abajo, la segunda la de arriba-izquierda, la tercera la de arriba-derecha y la cuarta la de abajo-derecha. Las llamaremos seccion1, seccion2, seccion3 y seccion4, respectivamente.
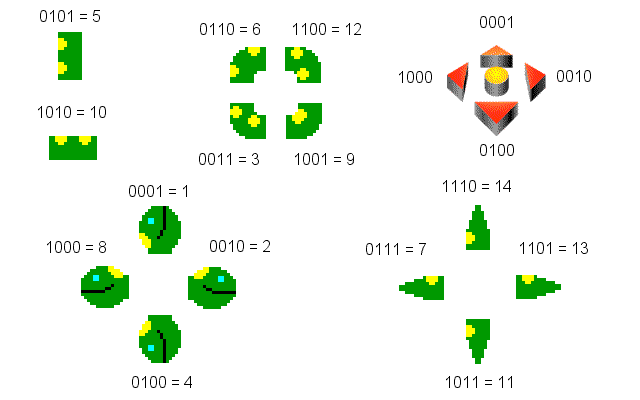
Para las dos secciones restantes: cabeza y cola, usaremos los demás valores posibles mediante suma de direcciones, por ejemplo, 1, 2, 4 y 8 para la cabeza. Para la cabeza mantendremos la mísma lógica de direcciones. Para la cola usaremos los valores 7, 11, 13 y 14, usando lógica inversa, es decir, codificando la dirección con ceros en lugar de con unos.
Para las direcciones definiremos un tipo enumerado siguiendo la misma lógica: eDireccion.
Así, si tenemos que determinar el tipo de una sección, sólo tenemos que sumar los valores de la dirección de procedencia y de la nueva dirección. Si la serpiente venía de abajo y gira a la izquierda, sumaremos los valores de abajo e izquierda:
4+8=12, es decir, la Seccion1.
Pero cuidado, porque en este cálculo hemos usado la dirección de procedencia, y no la previa, que en este ejemplo sería arriba. Por lo tanto, para obtener el valor de una sección con los datos que tenemos hay que realizar algunos cálculos:
El valor de dirección contrario al previo más el valor de dirección actual.
Para calcular el valor contrario de una dirección usaremos dos rotaciones de bits, por ejemplo, para la dirección arriba, que tiene el valor 0001, la dirección contraria es 0001 << 2 = 0100, es decir: abajo. Cuando se trate de valores de dirección 1 ó 2 rotaremos a la izquierda, cuando sean 4 u 8, a la derecha.
En la clase "CDireccion" sobrecargaremos el operador ! para esta operación.
El cálculo de las nuevas secciones de cola es algo más complicado. Por ejemplo, supongamos que la serpiente termina con una sección recta y una de cola hacia abajo. En un momento dado eliminamos la sección de cola, y la última sección de la serpiente es ahora recta, por lo tanto tendremos que calcular el nuevo valor de la sección de cola basándonos en el valor actual de la última sección y el de la sección anterior a esa.
La cola y la cabeza sólo codifican una dirección, y cualquier otra sección codifica dos. Lo primero que haremos será aplicar una función and de bits entre los dos valores. Esto nos da la dirección que tienen en comun las dos secciones.
De ese valor obtenemos la dirección contraria aplicando el algoritmo que hemos visto antes, y el resultado lo complementamos a 1, es decir, sustituiremos los unos por ceros y los ceros por unos, para obtener el valor de la sección de cola correspondiente a la dirección obtenida. Esto es tan sencillo como restar el valor de 15.
Veamos un ejemplo:
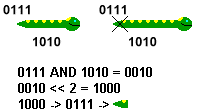
El valor de la sección de cola que vamos a eliminar es 0111. Si invertimos los bits de ese valor obtenemos 1000, que es el valor de la dirección izquierda.
El valor de la sección que pasará a ser cola es 1010, que codifica las direcciones izquierda y derecha. Aplicando la función AND obtenemos el valor 0010, es decir la dirección derecha. El valor contrario es 1000, de nuevo izquierda. Y el complementario es 0111, que es el valor de cola adecuado.
En el ejemplo anterior parece que nos complicamos la vida en exceso, veamos otro ejemplo:
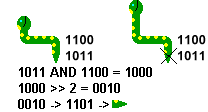
Ahora, el valor de la sección de cola que vamos a eliminar es 1011. Si invertimos los bits de ese valor obtenemos 0100, que es el valor de la dirección abajo.
El valor de la sección que pasará a ser cola es 1100, que codifica las direcciones izquierda y abajo. Aplicando la función AND obtenemos el valor 1000, es decir la dirección izquierda. El valor contrario es 0010, o sea derecha. Y el complementario es 1101, que es el valor de cola adecuado.
Podríamos haber hecho esto mismo con tablas que codificaran todos los casos posibles, pero considero que siempre es mejor calcular los valores que memorizarlos. En este caso se trata de operaciones sencillas: sumas, restas y operaciones lógicas, y se trata de cálculos muy rápidos.
Pero además, nos interesa añadir algunos refinamientos gráficos para dar más vistosidad al juego. Cuando la serpiente coma algo, podemos hacer que se note un abultamiento en la coordenada en la que estaba la comida. Esto no requiere demasiados cálculos.
En lo que se refiere a los gráficos, bastará con añadir un quinto bit. La presencia de ese bit indica que en esa sección hay abultamiento, o en el caso de la cabeza, que la boca está abierta. La ausencia del bit indica que es una sección normal.
Por lo tanto, cuando calculemos una nueva sección tendremos en cuenta que el quinto bit se "hereda", tanto cuando sea la segunda sección como cuando calculemos la cola, que son los únicos casos en los que modificaremos los códigos de una sección.
Por ejemplo:
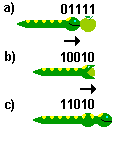
En la transición de (a) a (b), para calcular la sección correspondiente tomamos el valor de la dirección, 2, y como se trata de una casilla con comida le añadimos el quinto bit, es decir 10010.
En la transición de (b) a (c), la dirección sigue siendo derecha, y el valor previo de la sección es 10010. Ya vimos que se toma el valor de la dirección contraria a la previa más el valor de dirección actual.
Previamente recordamos el valor del quinto bit del valor de la sección actual, eso se hace comparando ese valor con 16 ó 0x10.
El valor de dirección previa coincide con los cuatro bits de la derecha del valor previo de la sección, es decir 10010 AND 01111 = 00010.
El valor contrario es 01000, y esto sumado con el valor de dirección es: 01000 + 0010 = 01010.
Por último, añadimos el valor del quinto bit que hemos memorizado 10000 + 01010 = 11010.
Otro ejemplo:
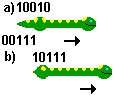
En la transición de (a) a (b), para calcular la sección correspondiente tomamos el valor de la penúltima sección y el de la sección de cola. La sección de cola se elimina, y para la otra calculamos un nuevo valor.
El valor de la sección de cola que vamos a eliminar es 00111. Si invertimos los bits de ese valor, prescindiendo del quinto, que no nos interesa de momento, obtenemos 1000, que es el valor de la dirección izquierda.
El valor de la sección que pasará a ser cola es 11010, que codifica las direcciones izquierda y derecha, y además indica que se trata de una sección ancha. Aplicando la función AND obtenemos el valor 00010, es decir la dirección derecha. El valor contrario es 01000, de nuevo izquierda. Y el complementario es 00111, que es el valor de cola adecuado.
Como previamente el valor de esa sección tenía el quinto bit a uno, conservamos ese bit, y se lo añadimos al valor calculado, 10000 | 00111 = 10111.
Comidas extra
A intervalos irregulares de tiempo se mostrarán comidas extra. Estas comidas tienen una diferencia importante con las normales: su periodo de vida es limitado, y el valor en puntos (y en crecimiento) que aporta depende de cuanta vida le quede, cuanto más pronto se coman, más puntos aportan.
En muchos aspectos se comportan como las comidas normales, se obtiene una coodenada libre para ella del laberinto. Pero a partir de ese momento el tiempo que le queda por permanecer en el laberinto empieza a disminuir. Además, mientras no hay ningún extra presente, también tendremos que disminuir otro contador que indica el tiempo que queda para que aparezca otra comida extra.
Para eso usamos el mismo temporizador que para el movimiento, cada vez que se ejecute la rutina del temporizador, además de actualizar la posición de la serpiente, decrementaremos el tiempo que le queda al extra para aparecer, si no está presente, o para desaparecer, si lo está.
No dispondremos de gráficos para todos los estados intermedios durante la presencia del extra en pantalla, de modo que sólo cambiaremos el gráfico cada cuatro estados. Como vamos a crear 16 gráficos, eso proporcionará un total de 64 estados. Cada estado corresponderá con un movimiento de la serpiente.
Tampoco queremos que los extras aparezcan demasiado a menudo, su función es no dejar al jugador organizarse demasiado, de modo que el juego no se convierta en algo aburrido. Los extras introducen nuevos objetivos que además tienen más preferencia, ya que dan más puntos y hay un tiempo limitado para conseguirlos. Eso obliga a cambiar las trayectorias lógicas por otras más cortas, y aumenta la dificultad. A veces puede ser mejor dejar pasar un extra que intentar conseguirlo, y por ese motivo no debemos hacer que sean muy frecuentes. Si el jugador sabe que pronto habrá otro extra, la prioridad por conseguirlo disminuirá.
Los tiempo para que aparezcan nuevos extras serán aleatorios, pero siempre estarán entre un máximo no demasiado alto y un mínimo no demasiado bajo. En nuestro caso entre 150 y 200 estados, pero eso puede cambiarse fácilmente.
Gráficos
La parte de diseño gráfico es para mi una de las más complicadas, y supongo que debe pasarle lo mismo a muchos programadores, ya que la mayoría de los gráficos de juegos son creados por especialistas, y muy rara vez por los mismos programadores.
Afortunadamente nuestro juego no es muy complicado, y el repertorio de gráficos es muy limitado. De modo que podemos atrevernos a diseñar unos gráficos sencillos, aunque puedan resultar toscos.
Necesitamos los gráficos de las cuatro secciones circulares, la vertical, la horizontal y cuatro versiones de cabeza y otras cuatro de cola, según las cuatro orientaciones posibles.
Además, debemos añadir un gráfico para la sección vacía, otro para la comida, y otro para los muros del laberinto.
Para dar más vistosidad al juego, hemos añadido versiones de todas las secciones de la serpiente que simulen que hay comida en su interior. Esto no complicará mucho el programa, y le añadirá vistosidad. En cuanto a la codificación, simplemente usaremos un quinto bit para indicar la presencia de comida en el interior de la serpiente, o lo que es lo mismo, sumaremos 16.
Por ejemplo, si la sección de cabeza apuntando arriba es la número 1, la sección equivalente con comida es la 17. Expresado en binario sería: 00001 y 10001. Lo mismo pasa con todas las secciones.
Además, esos números son los mismos que el número de orden dentro del mapa de bits, de modo que como cada gráfico es de 16x16 bits, para obtener la coordenada x de una sección cualquiera, bastará con multiplicar su valor por 16.

También tendremos que diseñar gráficos para los extras.
En este caso usaremos una fila para cada extra, y 16 versiones de cada uno dependiendo del tiempo. Esto nos permite añadir fácilmente más extras, si queremos.

Es muy sencillo obtener las coordenadas de un gráfico cualquiera, la coordenada x corresponde con el tiempo, siempre multiplicando por 16, ya que los gráficos siguen siendo de 16x16 bits. La coordenada y depende del gráfico elegido, también multiplicando por 16.
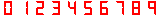
Además, añadiremos gráficos para los dígitos del contador. Seguiremos usando un único mapa de bits para todos los dígitos, también de 16x16 bits.

Y para el tablero de puntuaciones:
Resulta mucho más práctico usar un único mapa de bits para almacenar todos los gráficos. Las funciones para visualizar mapas de bits en Windows permiten seleccionar una zona concreta del mapa de bits, de modo que podemos extraer la zona que queramos.