Algoritmo de compresión de Huffman

Generalidades

Se trata de un algoritmo que puede ser usado para compresión o encriptación de datos.

Este algoritmo se basa en asignar códigos de distinta longitud de bits a cada uno de los caracteres de un fichero. Si se asignan códigos más cortos a los caracteres que aparecen más a menudo se consigue una compresión del fichero.

Esta compresión es mayor cuando la variedad de caracteres diferentes que aparecen es menor. Por ejemplo: si el texto se compone únicamente de números o mayúsculas, se conseguirá una compresión mayor.

Para recuperar el fichero original es necesario conocer el código asignado a cada carácter, así como su longitud en bits, si ésta información se omite, y el receptor del fichero la conoce, podrá recuperar la información original. De este modo es posible utilizar el algoritmo para encriptar ficheros.

Mecanismo del algoritmo

• Contar cuantas veces aparece cada carácter en el fichero a comprimir. Y crear una lista enlazada con la información de caracteres y frecuencias.
• Ordenar la lista de menor a mayor en función de la frecuencia.
• Convertir cada elemento de la lista en un árbol.
• Fusionar todos estos árboles en uno único, para hacerlo se sigue el siguiente proceso, mientras la lista de árboles contenga más de un elemento:
  • Con los dos primeros árboles formar un nuevo árbol, cada uno de los árboles originales en una rama.
  • Sumar las frecuencias de cada rama en el nuevo elemento árbol.
  • Insertar el nuevo árbol en el lugar adecuado de la lista según la suma de frecuencias obtenida.
• Para asignar el nuevo código binario de cada carácter sólo hay que seguir el camino adecuado a través del árbol. Si se toma una rama cero, se añade un cero al código, si se toma una rama uno, se añade un uno.
• Se recodifica el fichero según los nuevos códigos.

Veamos un ejemplo

Tomemos un texto corto, por ejemplo:

"ata la jaca a la estaca"

1) Contamos las veces que aparece cada carácter y hacemos una lista enlazada:

' '(5), a(9), c(2), e(1), j(1), l(2), s(1), t(2)

2) Ordenamos por frecuencia de menor a mayor

e(1), j(1), s(1), c(2), l(2), t(2), ' '(5), a(9)

3) Consideremos ahora que cada elemento es el nodo raíz de un árbol.

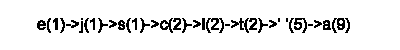
4) Fundimos los dos primeros nodos (árboles) en un nuevo árbol, sumamos sus frecuencias y lo colocamos en el lugar correspondiente:

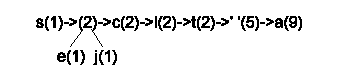
Y sucesivamente:

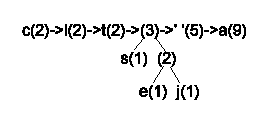
El resultado final es:

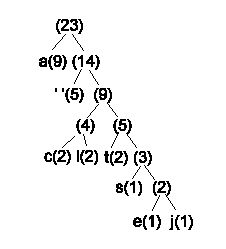
5) Asignamos los códigos, las ramas a la izquierda son ceros, y a la derecha unos (por ejemplo), es una regla arbitraria.

6) Y traducimos el texto:

Y sólo queda empaquetar los bits en grupos de ocho, es decir en bytes:

En total ocho bytes, y el texto original tenía 23.

Pero no nos engañemos, también hay que almacenar la información relativa a la codificación, por lo que se puede ver que para textos cortos no obtendremos mucha reducción de tamaño.

Programas en C

Bueno, y ahora la implementación en C.

Hay dos programas:

Nombre	Fichero	Fecha	Tamaño	Contador	Descarga
Compresor	Compres.zip	2001-02-01	10060 bytes	1307

Nombre	Fichero	Fecha	Tamaño	Contador	Descarga
Descompresor	Decomp.zip	2001-02-01	4850 bytes	925