Combinaciones

Combinaciones sin repetición de n elementos tomados de r en r

Mientras escribía el código para buscar grupos de casillas para resolver sudokus me encontré ante el problema de generar sucesivamente todas las combinaciones de varias casillas que cumplieran ciertas condiciones. En el caso concreto de los sudokus siempre se trata de conjuntos de nueve casillas, y los grupos varían en tamaño entre dos y siete.

De ahí surgió una plantilla C++ para crear todas las posibles combinaciones sin repetición de r elementos desde un conjunto de n elementos.

La fórmula para calcular el número de combinaciones posibles es:

$$\underset{C}{\overset{r}{n}}\frac{\mathrm{n!}}{{\mathrm{(n-r)!\; r!}}^{}}$$

Ten en cuenta que la imagen que ilustra este artículo no se corresponde con este tipo de combinaciones, ya que cada rueda del candado tiene diez elementos, y esos elementos se pueden tomar de tres en tres, pero se permiten repeticiones de elementos, de modo que las combinaciones posibles son 10³, es decir, 1000.

Si no pudiéramos repetir elementos, las combinaciones son, según la fórmula anterior, 120.

En el caso de nuestro sudoku, por ejemplo, las combinaciones de nueve casillas para formar grupos de tres son 84.

Algoritmo

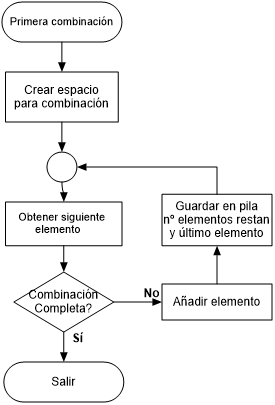
Dividiremos el algoritmo en dos partes.

La primera combinación se obtiene de una forma diferente al resto, ya que tendremos que establecer algunos parámetros iniciales, el número de elementos de cada combinación y el espacio para almacenar la combinación que se está obteniendo. Estos valores serán los mismos para el resto de las combinaciones a obtener.

Nuestro primer algoritmo es Primera, al que pasaremos como parámetro el valor de r.

Obtenemos espacio para almacenar la combinación en Elemento.

Empezamos ahora la parte recursiva, correspondiente al algoritmo Siguiente elemento, con dos parámetros (s,i): El primer parámetro ses el número de elementos que quedan por determinar en la combinación actual, que inicialmente son todos, es decir, r. El segundo parámetro i, es el índice del siguiente elemento del conjunto a incluir en la combinación, inicialmente el primero, o sea 0.

El algoritmo de Siguiente elemento es:

• Si el número de elementos que quedan por determinar es cero, s==0, habremos terminado de obtener la combinación y regresamos con un valor que indique que tenemos una combinación válida, por ejemplo, true.
• En caso contrario:
  • Guardamos en la pila los parámetros recibidos, (s,i).
  • Fijamos el valor del elemento r-s, con el valor del elemento v[i].
  • Invocamos de nuevo el procedimiento Siguiente elemento con los parámetros (s-1, i+1), es decir, indicando que nos queda un elemento menos por determinar, y que el siguiente elemento a elegir es i+1.

Por ejemplo, si partimos de un conjunto v de cinco letras, {a, b, c, d, e}, con los índices de 0 a 4, y queremos obtener las combinaciones de tres elementos, comenzaremos por almacenar el valor r igual a 3 para el número de elementos de cada combinación y consiguiendo memoria para almacenar tres letras en Elemento.

La primera combinación empieza con la llamada a Siguiente elemento con los parámetros (r,i), con los valores (3,0). 3 es distinto de 0, así que guardamos en la pila los valores (3,0), fijamos el elemento[r-s]=v[i] es decir, elemento[0]=v[0], y volvemos a invocar a Siguiente elemento con los parámetros (s-1, i+1), o sea (2,1).

Ahora s es 2, sigue siendo distinto de 0. Guardamos en la pila los valores (2,1), y asignamos elemento[r-s]=v[i], es decir, elemento[1]=v[1] y volvemos a llamar a Siguiente elemento con los parámetros (s-1, i+1), o sea (1,2).

De nuevo s es 1, sigue siendo distinto de 0. Guardamos en la pila los valores (1,2), y asignamos elemento[r-s]=v[i], es decir, elemento[2]=v[2] y volvemos a llamar a Siguiente elemento con los parámetros (s-1, i+1), o sea (0,3).

Esta vez s es 0, de modo que tenemos una combinación completa, y regresamos. En elemento tenemos los valores {a, b, c}, y en la pila las parejas {(3,0), (2,1), (1,2)}.

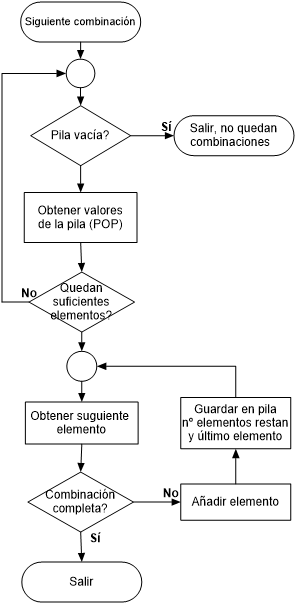
Cuando queramos obtener las siguientes combinaciones usaremos un segundo algoritmo.

• Empezamos verificando si quedan valores en la pila, si no queda ninguno significa que ya no quedan combinaciones por encontrar y retornamos un valor que lo indique, por ejemplo, false.
• Si quedan elementos en la pila, obtenemos el siguiente valor para (s,i).
• Ahora tenemos que asegurarnos de que quedan suficientes elementos en el conjunto de entrada para completar la combinación actual. Nos quedan por fijar s elementos, y nuestro conjunto tiene n elementos, por lo tanto, n-s debe ser mayor que i, o de otro modo nos quedaremos sin elementos en el conjunto de entrada para completar una combinación.
  • Si no quedan suficientes elementos, i>=n-s, significa que la no hay más combinaciones con los elementos que contiene actualmente elemento, asú que llamaremos a Siguiente.
  • Si quedan suficientes, tendremos que obtener el siguiente elemento de la combinación actual, llamando a Siguiente elemento con los parámetros (s, i+1).

Sigamos con nuestro ejemplo:

En la pila quedan tres elementos, de modo que sacamos el último, (1,2).

Verificamos la expresión i<n-s, es decir, 2<5-1. La expresión es verdadera, así que llamamos a Siguiente elemento con los parámetros (1,3).

Ahora s es 1, que es distinto de 0. Guardamos en la pila los valores (1,3), y asignamos elemento[r-s]=v[i], es decir, elemento[2]=v[3] y volvemos a llamar a Siguiente elemento con los parámetros (s-1, i+1), o sea (0,4).

Esta vez s es 0, de modo que tenemos una combinación completa, y regresamos. En elemento tenemos los valores {a, b, d}, y en la pila las parejas {(3,0), (2,1), (1,3)}.

Para la siguiente combinación en elemento tenemos los valores {a, b, e}, y en la pila las parejas {(3,0), (2,1), (1,4)}.

Si pedimos otra combinación, en la pila siguen quedando tres elementos, así que sacamos el último, (1,4).

Pero ahora la expresión i<n-s, es decir, 4<5-1, ya no se cumple, de modo que volvemos a llamar a Siguiente.

En la pila quedan ahora dos elementos, así que sacamos el último, (2,1).

La expresión i<n-s, es decir, 1<5-2, sí se cumple, de modo que llamamos a Siguiente elemento con los parámetros (2,2).

Ahora s es 2, que es distinto de 0. Guardamos en la pila los valores (2,2), y asignamos elemento[r-s]=v[i], es decir, elemento[1]=v[2] y volvemos a llamar a Siguiente elemento con los parámetros (s-1, i+1), o sea (1,3).

Con s es 1, que es distinto de 0. Guardamos en la pila los valores (1,3), y asignamos elemento[r-s]=v[i], es decir, elemento[2]=v[3] y volvemos a llamar a Siguiente elemento con los parámetros (s-1, i+1), o sea (0,4).

Esta vez s es 0, de modo que tenemos una combinación completa, y regresamos. En elemento tenemos los valores {a, c, d}, y en la pila las parejas {(3,0), (2,2), (1,3)}.

Para la última combinación tendremos para elemento los valores {c, d, e}, y en la pila las parejas {(3,2), (2,3), (1,4)}.

Si pedimos otra combinación, en la pila siguen quedando tres elementos, así que sacamos el último, (1,4).

Ahora la expresión i<n-s, es decir, 4<5-1, ya no se cumple, de modo que volvemos a llamar a Siguiente.

En la pila siguen quedando dos elementos, así que sacamos el último, (2,3).

La expresión i<n-s, es decir, 3<5-2, tampoco se cumple, de modo que volvemos a llamar a Siguiente.

En la pila sigue quedando un elemento, así que lo sacamos (3,2).

La expresión i<n-s, es decir, 2<5-3, tampoco se cumple, de modo que volvemos a llamar a Siguiente.

Ya no quedan elementos en la pila, así que regresamos con false para indicar que no quedan más combinaciones posibles.

Código

Hemos implementado el algoritmo en forma de plantilla, de modo que se pueda usar con conjuntos de cualquier tipo, almacenados en arrays, para generar combinaciones de cualquier tamaño.

También hemos usado la estructura para la pila de STL stack, que nos simplifica mucho la tarea.

El código resultante es bastante compacto:

// Generador de combinaciones sin repetición
// Guardar como combinaciones.h
// (C) 2023 Salvador Pozo
// Con Clase https://conclase.net

// Usamos la pila de STL
#include <stack>

template<class T> class Combinacion {
private:
    // Clase privada para almacenar valores en la pila
    class par {
    private:
        int nElementos, indice;
    public:
        par(int n=0,int i=0) : nElementos(n), indice(i) {}
        int NElementos() { return nElementos; }
        int Indice() { return indice; }
    };
    T *valor; // Valores del conjunto
    T *comb; // Valores de la combinación actual
    int nElementos; // Nº de elementos del conjunto
    int grupo; /Nº de elementos de cada combinación
    par pareja;
    std::stack<par> pila;

public:
    Combinacion(T *v, int n) : nElementos(n), grupo(0), pila() {
        valor = new T[nElementos];
        for(int i=0; i<nElementos; i++) valor[i] = v[i];
    }
    ~Combinacion() {
        delete[] valor;
        delete[] comb;
    }
    // Si queremos empezar de nuevo a generar combinaciones, con
    // el mismo número de elementos u otro, hay que liberar y volver
    // o obtener memoria para la combinación actual
    bool PrimeraCombinacion(int tam) {
        if(grupo) delete[] comb;
        grupo = tam;
        comb = new T[grupo];
        return SiguienteElemento(tam,0);
    }
    bool SiguienteElemento(int ne, int i) {
        if(ne > 0) {
            pila.push(par(ne, i));
            comb[grupo-ne] = valor[i];
            SiguienteElemento(ne-1, i+1);
        }
        return true;
    }
    bool SiguienteCombinacion() {
        if(pila.empty()) return false;
        pareja = pila.top();
        pila.pop();
        if(pareja.Indice() < nElementos-pareja.NElementos()) {
            return SiguienteElemento(pareja.NElementos(), pareja.Indice()+1);
        } else {
            return SiguienteCombinacion();
        }
    }
    const T *Comb() const { return comb; }
};

Para probar el funcionamiento:

// Generador de combinaciones sin repetición
// (C) 2023 Salvador Pozo
// Con Clase https://conclase.net

#include <iostream>
#include "combinaciones.h"

int main() {
    int v[9] = {1,2,3,4,5,6,7,8,9};

    Combinacion<int> grupo(v,9);

    std::cout << "Combinaciones de 3 elementos:" << std::endl;
    int i = 1;
    if(grupo.PrimeraCombinacion(3))
        do {
            std::cout << i++ << ") ";
            for(int i=0; i<3; i++) std::cout << grupo.Comb()[i]; // Combinaciones de tres elementos
            std::cout << std::endl;
        } while(grupo.SiguienteCombinacion());

    std::cout << "Combinaciones de 4 elementos:" << std::endl;
    i = 1;
    if(grupo.PrimeraCombinacion(4))
        do {
            std::cout << i++ << ") ";
            for(int i=0; i<4; i++) std::cout << grupo.Comb()[i]; // Combinaciones de tres elementos
            std::cout << std::endl;
        } while(grupo.SiguienteCombinacion());

    char c[6] = {'a','e','i','o','u'};
    Combinacion<char> grupo2(c,5);

    std::cout << "Combinaciones de 3 elementos:" << std::endl;
    if(grupo2.PrimeraCombinacion(3))
        do {
            for(int i=0; i<3; i++) std::cout << (char)grupo2.Comb()[i]; // Combinaciones de tres elementos
            std::cout << std::endl;
        } while(grupo2.SiguienteCombinacion());

    return 0;
}