Cálculo de trayectorias en colisiones

Como parte del curso de SDL 2 estamos programando una versión del juego clásico Asteroids.
Pero he querido añadir algunas físicas que hagan el juego más interesante, por ejemplo, que cuando las trayectorias de dos asteroides se crucen no se limiten a pasar uno sobre otro, sino que reboten como lo harían si fuesen bolas de billar, es decir, un choque elástico.
Pero no nos limitaremos a rebotar los asteroides en direcciones aleatorias, queremos que las direcciones sean realistas, o sea, que sigan las reglas físicas de las colisiones en dos dimensiones.
Para calcular las trayectorias y velocidades de dos objetos después de una colisión tenemos que conocer sus masas y sus velocidades y direcciones antes de la colisión.
No será necesario conocer las masas reales, bastará con conocer la proporción entre las masas de los dos objetos. Por ejemplo, si uno de los objetos tiene una masa M1 y el otro una masa M2, el valor que nos interesa es M1/M2.
Antes de plantearnos el problema del choque o colisión entre dos objetos, podemos resolver situaciones más simples.
Impulso
El impulso se define como una fuerza aplicada a lo largo de un tiempo. Por ejemplo, un objeto que se deja caer recibe un impulso constante debido a la fuerza de la gravedad. Para que la velocidad de un objeto cambie debe recibir un impulso, I. Aquí interviene la segunda ley de Newton, que nos dice que la fuerza neta aplicada a un objeto es proporcional a la aceleración que adquiere.
I = F·Δ t
Otro concepto que nos interesa en el momento o cantidad de movimiento, que se define como el producto de la masa por la velocidad. Al ser la velocidad un vector, el momento también lo es.
p = m·v
Podemos decir entonces que cuando se aplica un impulso a un objeto su velocidad cambiará. Tanto el impulso (que es una fuerza) como la velocidad son valores vectoriales, de modo que podemos expresar el impulso como la diferencia entre los momentos antes y después de aplicarlo:
I = m·vf−m·vf
En ausencia de impulso no habrá aceleración, y por lo tanto, tampoco se modificará la velocidad del objeto, que es lo que dice la primera ley de Newton. En ausencia de fuerzas externas, un objeto conservará su dirección y velocidad.
Colisiones con una superficie
La experiencia (y la experimentación) nos dice que si un objeto choca con una trayectoria perpendicular con una superficie, después de la colisión se moverá en la misma dirección, pero en sentido contrario y a menor velocidad. Por ejemplo, una pelota que cae desde cierta altura desde una posición de reposo, después de chocar contra el suelo volverá a subir, pero no llegará a la misma altura de la que partió. La velocidad de rebote dependerá de la energía que el objeto recupere después de la colisión.
En realidad, en la colisión de un objeto contra una superficie están implicados dos objetos, ya que la superficie lo es de un objeto mucho más grande, que podemos simplificar como de masa infinita, aunque solo lo es de una magnitud comparada tan grande que podemos considerarlo inamovible, y para nuestro caso ideal también indeformable.
Antes de chocar el objeto tendrá una energía cinética, proporcional a su masa y a su velocidad, concretamente en proporción a (m·v2)/2.
Durante la colisión toda esa energía se almacena mediante la deformación de los objetos implicados en el choque. De nuevo, nuestra pelota se aplastará contra el suelo, y cuando toda la energía cinética se haya consumido en esa deformación, la pelota volverá a recuperar su forma, liberando la energía acumulada, y volviendo a ganar velocidad en dirección contraria.
La velocidad del objeto después del rebote será menor que la que tenía después, y dependerá de cuánta energía almacenada en la deformación pueda ser convertida de nuevo en movimiento. Siempre habrá alguna pérdida en forma de calor, deformación permanente, sonido, etc. La relación entre la velocidad después y antes de la colisión se denomina coeficiente de restitución, y tiene signo negativo, ya que la dirección de la velocidad se invierte: ε = -vf/vi.
En nuestro ejemplo de la pelota deberemos fijarnos únicamente en las velocidades inmediatamente antes y después de la colisión, ya que en el resto del tiempo también interviene una fuerza externa: la gravedad.
Si el coeficiente de restitución es -1 hablaremos de colisiones elásticas, donde toda la velocidad antes de la colisión se recupera después de ella. Cuando es 0 hablaremos de colisiones inelásticas. Entre unas y otras se situarán todas aquellas que tengan un coeficiente entre 0 y -1, las colisiones semielásticas.
Por ejemplo, si en lugar de una pelota soltamos una bola de arcilla, la velocidad después de la colisión será nula, y la bola de arcilla permanecerá deformada, aplastada contra el suelo.
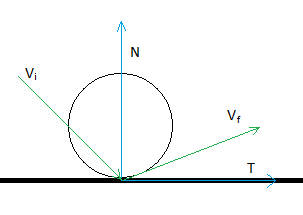
Un caso más general es que el objeto se mueva en una dirección que no sea perpendicular a la superficie de colisión. En nuestro ejemplo, la pelota se mueve porque se la hemos lanzado a otro jugador, como pasa en el tenis.
Podemos descomponer la velocidad, que es un vector ya que posee una magnitud y una dirección, en dos componentes. Una perpendicular a la superficie de colisión y la otra paralela. A la dirección perpendicular a la superficie de colisión la denominamos normal y a la paralela tangencial.
En la dirección tangencial no interviene ninguna fuerza, por lo tanto, la velocidad tangencial antes y después de la colisión permanecerá constante.
vit = vft
En cuanto a la componente normal, estamos en el mismo caso que la colisión perpendicular a la superficie, por lo que podemos aplicar la misma fórmula para la componente normal:
vfn = -ε· vin
Colisiones de dos objetos en una dimensión
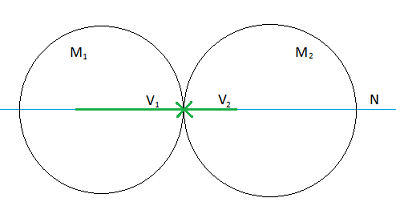
Ahora supongamos que tenemos dos objetos que se mueven en la misma dirección y en sentidos contrarios. En el momento de la colisión no existen impulsos externos, por lo tanto, se conservará la cantidad de movimiento del conjunto.
m1·v1i+m2·v2i = m1·v1f+m2·v2f
Si se trata de una colisión elástica, la energía cinética del conjunto también se mantiene, por lo tanto tenemos:
(m1·v21i)/2 + (m2·v22i)/2 = (m1·v21f)/2 + (m2·v22f)/2
Podemos calcular las velocidades finales de cada objeto a partir de estas fórmulas.
v1f = (v1i·(m1-m2)+2·v2i·m2)/(m1+m2) v2f = (v2i·(m2-m1)+2·v1i·m1)/(m1+m2)
En el caso particular de que ambos objetos tengan la misma masa tenemos:
v1f = 2·v2i·m/2·m = v2i v2f = 2·v1i·m/2·m = v1i
Es decir, se intercambian las velocidades.
Para colisiones no elásticas tenemos que tener en cuenta el coeficiente de restitución:
ε = -(m1v1f+m2v2f)/(m1v1i+m2v2i)
Y la fórmula de conservación del momento:
m1·v1i+m2·v2i = m1·v1f+m2·v2f
Haciendo algunos cálculos, a partir de estas fórmulas obtenemos:
v1f = (v1i·m1·(1+ε)+v2i·(m2-ε·m1))/(m1+m2) v2f = (v2i·m2·(1+ε)+v1i·(m1-ε·m2))/(m1+m2)
En el caso de que la colisión sea inelástica, el valor de ε es cero, y la velocidad final de los dos objetos será la misma, tanto en magnitud como en dirección:
v1f = (v1i·m1+v2i·m2)/(m1+m2) v2f = (v2i·m2+v1i·m1)/(m1+m2) v1f = v2f
Colisiones en dos dimensiones
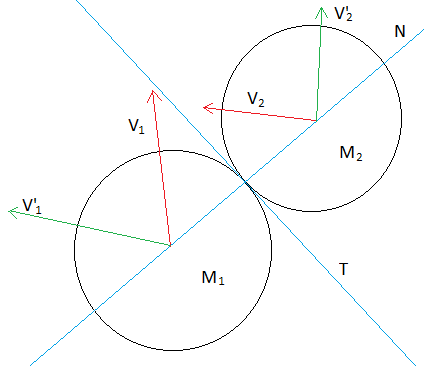
Tomemos por ejemplo la imagen de la derecha. Dos objetos chocan. El primero con una masa M1 y una velocidad y dirección definida por el vector V1, el segundo con una masa M2 y una velocidad y dirección definida por el vector V2.
Denominamos Normal a la línea que une los centros de los círculos, y que pasa por el punto de colisión. Perpendicular a la Normal tenemos otra línea, la Tangencial.
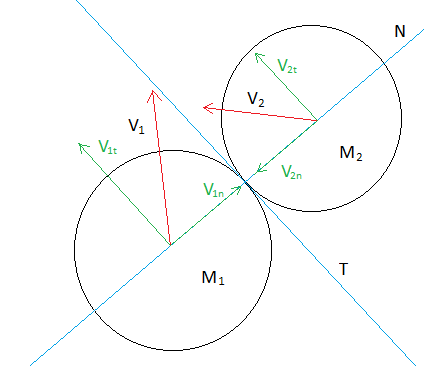
Podemos ahora tomar las líneas Normal y Tangencial como nuestros ejes de coordenadas y referir los vectores de velocidad a esos nuevos ejes. Ahora descompondremos las velocidades de los objetos en dos componentes, una paralela a la normal y la otra paralela a la tangencial.
Como en el caso de la colisión con una superficie, vemos que las componentes tangenciales de las velocidades antes y después de la colisión no varían, ya que no existe ninguna fuerza en esa dirección:
v1ft = v1it v2ft = v2it
A partir de la fórmula de conservación del momento:
m1·v1i+m2·v2i = m1·v1f+m2·v2f
Podemos aplicarla a las componentes normales:
m1·v1in+m2·v2in = m1·v1fn+m2·v2fn
Finalmente aplicaremos la ecuación del coeficiente de restitución para las componentes en la dirección normal:
ε = -(V'1n−V'2n)/(V1n+V2n)
Con las componentes normales estamos en el mismo caso que con las colisiones en una dimensión, de modo que podemos aplicar las mismas fórmulas.
v1fn = (v1in·m1·(1+ε)+v2in·(m2-ε·m1))/(m1+m2) v2fn = (v2in·m2·(1+ε)+v1in·(m1-ε·m2))/(m1+m2)
Para colisiones perfectamente elásticas el valor de ε es 1, por lo tanto, las fórmulas quedan:
v1fn = (2·v1in·m1+v2in·(m2-m1))/(m1+m2) v2fn = (2·v2in·m2+v1in·(m1-m2))/(m1+m2) v1ft = v1it v2ft = v2it
Aplicación en colisiones en juegos
En el curso de SDL 2 hablamos de la detección de colisiones y de hitboxes. Como veremos, para calcular rebotes nos conviene usar hitboxes circulares, lo que se adapta bastante bien a juegos como el billar o nuestra versión de Asteroids. Así que, independientemente de la forma del asteroide, para nuestros cálculos asumiremos que son circulares.
Las velocidades y direcciones de cada objeto después de una colisión dependen de la relación entre las masas de cada una y del coeficiente de restitución, que nos indica que tan elástica es una colisión. Si ese coeficiente es 1, diremos que la colisión es elástica, y tendremos un rebote perfecto; si es 0 diremos que es inelástica, y no habrá rebote. En el rango entre 0 y 1 tendremos las colisiones semielásticas, con comportamientos intermedios.
Independientemente del tipo de colisión el valor del impulso antes y después de la colisión se mantiene constante.
Las fórmulas que hemos deducido antes para calculas las componentes de las velocidades después de una colisión están referidas a un sistema de coordenadas que en general no será el mismo que usemos en el juego, por lo tanto será necesario hacer un cambio de coordenadas adicional.
Esto, en principio, complica los cálculos, ya que pasamos de cuatro a ocho ecuaciones, y recordemos que tendremos que calcular todos esos valores, en tiempo real, para cada colisión.
Pero un cambio del sistema de referencia en dos dimensiones solo implica hacer una rotación. Bastará con calcular el ángulo que forma la normal de la colisión con nuestro sistema de coordenadas, y realizar el giro correspondiente.
Ángulo de eje normal
Una vez detectada una colisión podemos calcular el ángulo que forma el plano de colisión y la normal con respecto a nuestros ejes cartesianos.
El ángulo normal es el arcotangente del cociente entre la diferencia de las coordenadas y la diferencia de las coordenadas x de los centros de los objetos.
Si las coordenadas de los objetos son (x1, y1) y (x2, y2), el ángulo de la normal es:
θ = atan((y2-y1)/(x2-x1))
Hay que recordar tener en cuenta el caso especial si la diferencia de las coordenadas x es cero, ya que no podemos dividir por cero. En ese caso, si la diferencia de coordenadas y es positiva el arco tangente será 90º, o π/2 radianes. Si es negativa será 270º o 3·π/2 radianes o -π/2 radianes.
Aunque recordemos que la librería estándar de C nos proporciona una función que es preferible en este caso. La función atan2 calcula el arcotangente a partir de dos parámetros, que son el numerador y denominador de la fracción anterior:
θ = atan2(y2-y1, x2-x1)
Cambio de coordenadas
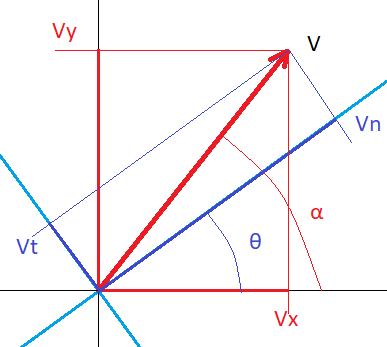
Para cada vector de velocidad tendremos que efectuar dos cambios de coordenadas, el primero para pasar la velocidad expresada en coordenadas del juego (Vx, Vy) a las coordenadas definidas por los ejes normal y transversal, (Vn, Vt). Para ello solo necesitamos saber el ángulo que forma nuestro eje x con la normal a la línea (o plano) de colisión.
Si optamos por hacer cálculos trigonométricos, podemos calcular el ángulo del vector con respecto al eje x de modo análogo al modo en que calculamos el ángulo de la normal:
α = atan2(Vx, Vy)
Las componentes con respecto a la normal y transversal son:
Vn = V · cos(α - θ) Vt = V · sin(α - θ)
Sin embargo esto nos obliga a calcular también la magnitud de la velocidad, V, que es la raíz cuadrada de la suma de los cuadrados de Vx y Vy. Y eso puede ralentizar los cálculos.

Pero podemos aplicar las fórmulas de rotación que ya hemos usado antes para rotar gráficos. De este modo, las nuevas coordenadas quedan:
Vn = Vx · cos(θ) + Vy · sin(θ) Vt = -Vx · sin(θ) + Vy · cos(θ)
Nota: Estas fórmulas de rotación son válidas para el sistema de coordenadas que se usan en juegos, en los que los valores de y crecen hacia abajo.
Aplicamos la misma rotación para la velocidad de los dos objetos y aplicamos las fórmulas que vimos antes para calcular las velocidades después de la colisión.
Si consideramos nuestras colisiones elásticas usaremos un valor de ε igual a 1.
v1fn = (2·v1in·m1+v2in·(m2-m1))/(m1+m2) v2fn = (2·v2in·m2+v1in·(m1-m2))/(m1+m2) v1ft = v1it v2ft = v2it
Y finalmente, volvemos a rotar las coordenadas a nuestro sistema, un ángulo de -θ. Recordemos que el coseno de θ es igual al coseno de -θ y el seno de θ es igual al menos el seno de -θ.
Vx = Vn · cos(θ) - Vt · sin(θ) Vy = Vn · sin(θ) + Vt · cos(θ)