Algebra de Boole (4)
Lógica secuencial
En artículos anteriores solo hemos visto funciones lógicas en las que el resultado depende exclusivamente de los valores de las entradas en un momento determinado. Es lo que se conoce como lógica combinatoria.
Por el contrario, en la lógica secuencial, el resultado de una función depende de los valores de las entradas y también de los valores pasados de esas entradas. Es decir, la lógica secuencial necesita recordar valores previos de las entradas, o lo que es lo mismo, necesita memoria.
Cuando se aplica a la electrónica digital, esta memoria se suele implementar mediante biestables, es decir, circuitos en que la salida admite dos estados estables, o que almacenan un bit de información. Las memorias de ordenador no son otra cosa que millones de estos circuitos biestables.
Existen varios tipos de biestables, y cuando se diseñan circuitos lógicos secuenciales hay que tener en cuenta el tipo de biestable que se usará, ya que sus funciones de entrada serán diferentes dependiendo del tipo.
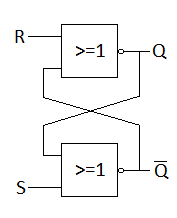
De hecho, cada tipo de biestable es en si mismo un circuito secuencial. Por ejemplo, un biestable RS tendrá dos estados, dos entradas y una o dos salidas. Las entradas, que dan el nombre al biestable son R, de reset y S de set, o sea apagado y encendido. Si se activa la entrada S el biestable pasa al estado 1, y la salida será 1, si se activa la entrada R el estado pasa a 0, y la salida será 0. Si no se activa ninguna entrada, el estado no cambia. La situación en que se activan ambas entradas no se contempla, y el estado o salida es indeterminado. En un biestable RS nunca deberían activarse ambas entradas.
Frecuentemente un biestable suele tiene dos salidas, en esos casos la segunda salida tendrá el valor contrario al de la primera.
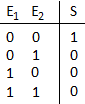
En el esquema del biestable RS la salida es Q, la segunda salida es Q negada, que se representa con una línea encima. Las cajas comparan los valores de entrada, y la salida de cada una es 1 si las dos entradas son 0, y 0 en cualquier otro caso. El círculo a la salida niega el resultado de la comparación. En realidad cada caja equivale a una operación lógica OR, en la que la salida es el complemento, o sea una operación lógica NOR.
La tabla de verdad de estas "cajas" es 1 cuando ambas entradas son 0 y 0 en el resto de casos.
Sincronismo
Además, los circuitos secuenciales se pueden clasificar en dos tipos: síncronos y asíncronos.
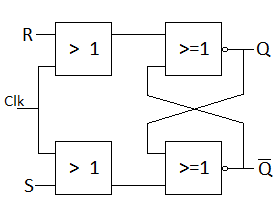
En los circuitos síncronos los cambios en las salidas y estados están gobernados por un reloj, en los asíncronos ese reloj no existe, y los cambios se producen tan pronto cambian los valores de las entradas.
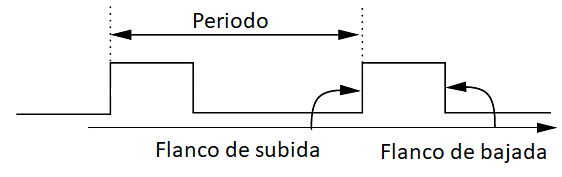
En lógica digital un reloj es una señal que cambia de un valor cero a uno y de uno a cero alternativamente a una frecuencia determinada. Su representación gráfica es una onda cuadrada. En concreto, para los circuitos secuenciales, de esa señal solo se suele utilizar uno de los flancos, o bien el de subida (cambio de cero a uno) o el de bajada (cambio de uno a cero). Da igual qué valor tengan las entradas el resto del tiempo, un circuito secuencial solo tendrá en cuenta el valor durante el flanco que se haya elegido como activo.
También pueden usarse los niveles en lugar de los flancos. Por ejemplo, en la imagen de la derecha se representa un biestable RS síncrono activo por nivel.
El ejemplo anterior de biestable RS es asíncrono, el valor de la salida se actualiza tan pronto se activa cualquiera de sus entradas.
Un ordenador no es otra cosa que un complejísimo circuito digital secuencial. Responde a las entradas (teclado, ratón, unidades de almacenamiento, entradas externas, etc) y a los estados previos (contenido de memoria), y da ciertas salidas.
Aunque lo que se explica en este artículo está orientado inicialmente a la electrónica digital, se puede utilizar para diseñar programas de ordenador o de microcontrolador. Nuestra señal de reloj es el bucle de programa, y nuestra memoria son variables.
Esto es mucho más útil cuando trabajamos con microcontroladores, en los que tenemos entradas y salidas digitales, y el programa principal es un único bucle que se repite indefinidamente. Por ejemplo, un programa de Arduino tiene esta forma:
void setup() {
// put your setup code here, to run once:
}
void loop() {
// put your main code here, to run repeatedly:
}
Donde la función setup se ejecuta una vez cuando el dispositivo se enciende, y la función loop se ejecuta a continuación repetidamente.
De hecho, salvo en problemas muy simples, actualmente es más frecuente usar microcontroladores para resolver problemas secuenciales que circuitería lógica con puertas y biestables.
Máquinas de estados finitos
Aunque las salidas en un momento determinado dependen de las entradas actuales y pasadas, no será necesario almacenar todas las entradas pasadas desde en inicio del funcionamiento. En la práctica, un circuito digital secuencial solo tiene que tener en cuenta un número determinado casos. Estos casos es lo que se denomina estados.

El tipo de problemas que se pueden resolver mediante lógica secuencial debe tener un número de estados posibles finito, por eso se conocen también estos circuitos como máquinas de estados finitos, o por sus siglas en inglés FSM. (Nada que ver con el Monstruo de Espagueti Volador del pastafarismo, ¡RAmén!)
Ciertas combinaciones de valores de entrada implican ciertos cambios de estado, y para cada estado, los valores de entrada implican ciertas salidas.
Veamos un ejemplo. Tenemos un ascensor en un edificio con cuatro plantas. En un momento dado, el ascensor solo puede estar en una de ellas, o sea , que tenemos cuatro posibles estados: E1, el ascensor está en la primera planta, E2, en la segunda, etc.
Si queremos diseñar el circuito para llamar al ascensor desde la primera planta, tenemos que tener en cuenta la entrada I1, que es el pulsador de llamada, y el estado del ascensor.
Las salidas serán dos, S1 para hacer subir al ascensor, y S2 para hacerlo bajar.
Los problemas que tendremos que resolver mediante lógica secuencial consistirán en determinar los estados posibles, el siguiente estado en función de las entradas y las salidas para cada estado.
Existen dos tipos de máquinas de estados finitos:
Máquina de Mealy
En este tipo máquinas las salidas son función de los estados y de los valores de entrada. A veces estas máquinas requieren menos estados que las de Moore.
Máquina de Moore
En estas máquinas las salidas solo dependen del estado en un momento dado. Son las transiciones las que dependen de las entradas y del estado en un momento dado.
Siempre se puede usar cualquiera de los dos tipos de máquinas, ya que hay una equivalencia entre ambas.
Diagramas de estados
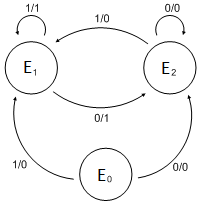
Los diagramas de estado son representaciones gráficas de los estados de una máquina de estados finitos, en las que se indican los valores de entrada que definen las transiciones entre estados y los valores de salida.
Es una de las primeras fases en la resolución de problemas de lógica secuencial y se suelen tomar como punto de partida para definir y simplificar las funciones que determinan los estados y las salidas.
En estos diagramas cada estado se representa con un nodo, y las transiciones entre estados se representan con las aristas dirigidas (flechas).
Se usan dos tipos de diagramas, dependiendo del tipo de problema que estemos resolviendo, de nuestras preferencias o de cual de los dos resulte óptimo.
Diagrama de Mealy
En este tipo de diagramas están asociados a máquinas de Mealy, en las que las salidas son función de los estados y de los valores de entrada. En cada arista se muestran los valores de las entradas y de las salidas, separadas con una '/'.
Diagrama de Moore
En estos diagramas, asociados a máquinas de Moore, las salidas solo dependen del estado. En cada arista solo se muestran los valores de las entradas.
Ejemplo 1
Veamos cómo funciona esto con un ejemplo sencillo.
Tenemos que manejar un sistema de calentamiento de agua mediante un panel solar. Para ello tenemos dos sondas de temperatura, una a la entrada del panel y otra a la salida. Para mover el agua tenemos una bomba, que será la salida de nuestro ejemplo.
No nos interesa que la bomba funcione si el panel no puede calentar el agua, por ejemplo, si está nublado o está en la sombra o es de noche. En esos casos esperaremos un tiempo y volveremos a probar.
Sin embargo, para medir la diferencia de temperatura a la entrada y salida del panel la bomba deberá estar en marcha, ya que si no circula agua por el panel, esa diferencia de temperatura será cero o muy pequeña, y la temperatura del agua a la entrada no será representativa de la que hay almacenada.
Además podemos agregar un control horario, de modo que el circuito pase a un estado diferente cuando sea de noche.
Nuestra salida S será el control de la bomba, 1 para activarla y cero para pararla.
La primera señal de entrada, I1, tendrá un valor falso (0), si la diferencia de temperatura a la entrada y a la salida es menor de 5ºC y será verdadera (1) si la temperatura a la salida es cinco o más grados mayor que la de entrada, siempre que la bomba esté en marcha. Con la bomba apagada no tendremos en cuenta las temperaturas que nos indiquen las sondas.
Una segunda señal de entrada, I2, será la salida de un temporizador programable de diez minutos. Su salida será falsa (0) si no se ha cumplido el tiempo, y verdadera (1) si han transcurrido diez minutos desde su inicio. Este es el tiempo que esperaremos cuando hayamos parado la bomba porque la diferencia de temperaturas a la salida y entrada sea inferior a 5ºC.
La tercera salida I3, será verdadera (1) durante las horas de sol y falsa (0) durante la noche.
En principio, con una versión simplificada del problema, tenemos tres estados:
- Si es de día, I3=1, en el estado de arranque ignoramos la entrada I1 lanzamos el temporizador. Mientras no se cumpla el tiempo de espera, I2=0, permaneceremos en ese estado.
- Una vez transcurrido el tiempo, I2=1, pasaremos al segundo estado y activaremos la bomba. Permaneceremos en ese estado mientras la temperatura a la salida sea cinco grados superior a la de entrada, I1=1. Si I1 pasa a valor 0, volveremos al estado inicial, y lanzaremos de nuevo el temporizador.
- Si es de noche, I3=0, ignoraremos cualquier otra entrada y pasaremos a un tercer estado, del que pasaremos al estado inicial si I3 vuelve a valer 1.
Hemos simplificado el problema de varias formas. Una simplificación consiste en que no vamos a tener en cuenta que después de arrancar la bomba hay que esperar un tiempo para que las lecturas de las sondas de temperatura sean fiables. Es posible que durante el tiempo de espera el panel se haya calentado, y al no circular el agua, las dos temperaturas, a la entrada y a la salida, sean muy parecidas y mucho más altas de la del agua almacenada.
Otra simplificación es que no hemos establecido una temperatura máxima, que en una situación real habría que tener en cuenta. Si lo que estamos calentando es el agua de una piscina, tal vez no queramos que su temperatura pase de 30ºC, si es un depósito de agua caliente para uso en una vivienda, podemos trabajar con temperaturas máximas de 50ºC o 60ºC.
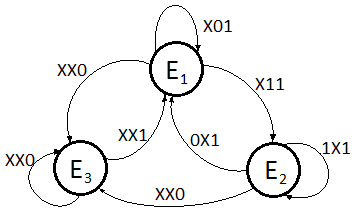
Diagrama
Como el valor de la salida depende del estado, solo estará activa en el segundo estado, usaremos una máquina de Moore.
Estableceremos los tres estados posibles, y añadiremos las aristas, indicando en cada una los valores de las variables de entrada, de derecha a izquierda: I1, I2 e I3.
Tabla de verdad
El resto del proceso para obtener las funciones lógicas es similar a lo que vimos anteriormente. Empezaremos por la tabla de verdad.
Nuestro circuito tendrá cinco entradas, I1, I2 e I3, y además los dos bits necesarios para codificar el valor del estado actual: Ei0 y Ei1. Y tendrá tres salidas, S que indica si se debe activar la bomba y los dos bits para codificar el valor del estado posterior: Eo0 y Eo1.
Es buena idea intentar optimizar la codificación de cada estado. En este ejemplo tenemos tres estados, de modo que necesitamos dos bits, que permiten codificar cuatro posibles estados: 00, 01, 10 y 11, así que nos sobra una codificación. Por otra parte, la bomba solo se activa en el estado 2, así que nos conviene usar para ese estado una de las codificaciones con un bit activo, 01 ó 10; y para los otros dos estados dos de las combinaciones que no usen ese bit. Es decir, si elegimos 01 para el estado 2, usaremos 00 y 10 para los estados 1 y 3, y si elegimos 10 para el estado 2, usaremos 00 y 01 para los estados 1 y 3.
Podría suceder que fuese más conveniente usar lógica negativa para activar la bomba, es decir, que se encienda con una salida con valor 0. En ese caso, si elegimos 01 para el estado 2, usaremos 10 y 11 para los estados 1 y 3, y si elegimos 10 para el estado 2, usaremos 01 y 11 para los estados 1 y 3.
Pongamos que elegimos 00 para el estado 1, 01 para el estado 2 y 10 para el estado 3. Tendremos esta tabla de verdad, en la que la función de salida coincide con el valor del bit 0 del estado:
| m | I1 | I2 | I3 | Ei1 | Ei0 | Eo1 | Eo0 | S |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 2 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| 3 | 0 | 0 | 0 | 1 | 1 | X | X | X |
| 4 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 6 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 7 | 0 | 0 | 1 | 1 | 1 | X | X | X |
| 8 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 9 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 10 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| 11 | 0 | 1 | 0 | 1 | 1 | X | X | X |
| 12 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 |
| 13 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 |
| 14 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 15 | 0 | 1 | 1 | 1 | 1 | X | X | X |
| 16 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 17 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 18 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| 19 | 1 | 0 | 0 | 1 | 1 | X | X | X |
| 20 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 21 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| 22 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 23 | 1 | 0 | 1 | 1 | 1 | X | X | X |
| 24 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 25 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 26 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| 27 | 1 | 1 | 0 | 1 | 1 | X | X | X |
| 28 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 |
| 29 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
| 30 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
| 31 | 1 | 1 | 1 | 1 | 1 | X | X | X |
Ahora podemos usar nuestro programa del artículo anterior para simplificar las funciones Eo1, Eo0 y S.
Eo0 = S = I1' I2' I3 E1 + I1 I3 E0 E01 = I3'
Esta resolución es válida para el diseño de circuitos lógicos, en los que los valores de estados se almacenan en memorias de un bit, pero cuando trabajemos con microcontroladores o programas en general, los estados se almacenarán en una variable.
Para usar estas funciones en un programa, por ejemplo, como condición de una sentencia if, tendremos que traducir los bits de estados a valores enteros. En este caso, los estados se codifican como:
| Estado | Bit 1 | Bit 0 |
|---|---|---|
| 1 | 0 | 0 |
| 2 | 0 | 1 |
| 3 | 1 | 0 |
Esto quiere decir que la condición E1 equivale al estado 3, E0 equivale al estado 2 y E1'E0' al estado 1.
Por otra parte:
- I1 indica que la diferencia de temperaturas entre la entrada y la salida del panel es mayor de 5ºC, llamaremos a esa variable deltaT. O podria ser una expresión como (T2-T1)>5.0.
- I2 indica que se ha cumplido el tiempo de espera en reposo, llamaremos a esa variable tiempo, o usar una expresión como tEspera==0.
- l3 indica que estamos en horario de sol, llamaremos a esa variable dia.
Podemos reescribir las funciones como:
Eo0 = S = !deltaT && !tiempo && dia && (estado==1) + deltaT && dia && (estado==2) Eo1 = !dia
Podemos extraer como factor común I3, o sea, dia:
Eo0 = S = dia && (!deltaT && !tiempo && (estado==1) || deltaT && (estado==2)) Eo1 = !dia
Pasado a código:
if(!dia) estado = 3;
else if(dia && (!deltaT && !tiempo && (estado==1) || deltaT && (estado==2))) estado = 2;
else estado = 1;
Por supuesto, en un programa usaremos un enumerado para codificar los estados:
enum tipoEstado {
espera,
trabajo,
noche
};
...
if(!dia) estado = noche;
else if(dia && (!deltaT && !tiempo && (estado==espera) || deltaT && (estado==trabajo))) estado = trabajo;
else estado = espera;
Este ejemplo es un caso sencillo, con pocos estados posibles, y se puede resolver de forma intuitiva usando una sentencia switch, pero con problemas que requieran muchos estados puede ser interesante una aproximación usando lógica secuencial.
Otra alternativa que puede ser más sencilla es crear una tabla diferente, creando una salida para cada valor de estado posible:
| Estado Inicial | Estado final | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| m | I1 | I2 | I3 | E1 | E2 | E3 | E1 | E2 | E3 | S |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | X | X | X | X |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 0 | 0 | 1 | 1 | X | X | X | X |
| 4 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 5 | 0 | 0 | 0 | 1 | 0 | 1 | X | X | X | X |
| 6 | 0 | 0 | 0 | 1 | 1 | 0 | X | X | X | X |
| 7 | 0 | 0 | 0 | 1 | 1 | 1 | X | X | X | X |
| 8 | 0 | 0 | 1 | 0 | 0 | 0 | X | X | X | X |
| 9 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 10 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 11 | 0 | 0 | 1 | 0 | 1 | 1 | X | X | X | X |
| 12 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 13 | 0 | 0 | 1 | 1 | 0 | 1 | X | X | X | X |
| 14 | 0 | 0 | 1 | 1 | 1 | 0 | X | X | X | X |
| 15 | 0 | 0 | 1 | 1 | 1 | 1 | X | X | X | X |
| 16 | 0 | 1 | 0 | 0 | 0 | 0 | X | X | X | X |
| 17 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| 18 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 19 | 0 | 1 | 0 | 0 | 1 | 1 | X | X | X | X |
| 20 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 21 | 0 | 1 | 0 | 1 | 0 | 1 | X | X | X | X |
| 22 | 0 | 1 | 0 | 1 | 1 | 0 | X | X | X | X |
| 23 | 0 | 1 | 0 | 1 | 1 | 1 | X | X | X | X |
| 24 | 0 | 1 | 1 | 0 | 0 | 0 | X | X | X | X |
| 25 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 26 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 27 | 0 | 1 | 1 | 0 | 1 | 1 | X | X | X | X |
| 28 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 29 | 0 | 1 | 1 | 1 | 0 | 1 | X | X | X | X |
| 30 | 0 | 1 | 1 | 1 | 1 | 0 | X | X | X | X |
| 31 | 0 | 1 | 1 | 1 | 1 | 1 | X | X | X | X |
| 32 | 1 | 0 | 0 | 0 | 0 | 0 | X | X | X | X |
| 33 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| 34 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 35 | 1 | 0 | 0 | 0 | 1 | 1 | X | X | X | X |
| 36 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 37 | 1 | 0 | 0 | 1 | 0 | 1 | X | X | X | X |
| 38 | 1 | 0 | 0 | 1 | 1 | 0 | X | X | X | X |
| 39 | 1 | 0 | 0 | 1 | 1 | 1 | X | X | X | X |
| 40 | 1 | 0 | 1 | 0 | 0 | 0 | X | X | X | X |
| 41 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 42 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 43 | 1 | 0 | 1 | 0 | 1 | 1 | X | X | X | X |
| 44 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 45 | 1 | 0 | 1 | 1 | 0 | 1 | X | X | X | X |
| 46 | 1 | 0 | 1 | 1 | 1 | 0 | X | X | X | X |
| 47 | 1 | 0 | 1 | 1 | 1 | 1 | X | X | X | X |
| 48 | 1 | 1 | 0 | 0 | 0 | 0 | X | X | X | X |
| 49 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| 50 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 51 | 1 | 1 | 0 | 0 | 1 | 1 | X | X | X | X |
| 52 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 |
| 53 | 1 | 1 | 0 | 1 | 0 | 1 | X | X | X | X |
| 54 | 1 | 1 | 0 | 1 | 1 | 0 | X | X | X | X |
| 55 | 1 | 1 | 0 | 1 | 1 | 1 | X | X | X | X |
| 56 | 1 | 1 | 1 | 0 | 0 | 0 | X | X | X | X |
| 57 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 58 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 59 | 1 | 1 | 1 | 0 | 1 | 1 | X | X | X | X |
| 60 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 61 | 1 | 1 | 1 | 1 | 0 | 1 | X | X | X | X |
| 62 | 1 | 1 | 1 | 1 | 1 | 0 | X | X | X | X |
| 63 | 1 | 1 | 1 | 1 | 1 | 1 | X | X | X | X |
De este modo aumentamos el número de entradas, pero debido a que hay más minterms redundantes, probablemente nuestras funciones simplificadas serán más sencillas. La salida S coincide con el estado 2, es decir las funciones S y Eo=2 son la misma.
Aplicando las simplificaciones a estas tablas obtenemos las siguientes funciones:
Eo1 = E1 I3 I2' + E3 I3 + E2 I3 I1' Eo2 = S = E2 I1 I3 + E1 I2 I3 Eo3 = I3'
Que usando los mismos nombres de variables que en el ejemplo anterior, podríamos codificar como:
if(!dia) Estado = 3;
else if(dia && ((Estado==2) && deltaT) || ((Estado==1) && tiempo)) Estado = 2;
else Estado = 1;
Notas
Por supuesto, en circuitos lógicos, podemos necesitar calcular más funciones, dependiendo del tipo de biestables que se usen. Por ejemplo, para un biestable RS tendremos que calcular una función R y una S para cada bit de estado.
Pero existen más tipos de biestables., por ejemplo:
- Biestables D: sencillamente almacenan un bit y solo tienen una entrada D. El valor de la entrada se almacenará en el siguiente ciclo de reloj. Estos biestables son los más útiles en circuitos secuenciales, ya que sólo necesitan un valor de entrada, además del reloj. Las funciones que hemos calculado se pueden usar con biestables tipo D.
- Biestables T: cambian el valor de la salida si la entrada T está activa en el siguiente ciclo de reloj.
- Biestables JK: funcionan como los RS, donde J equivale a Set y K a Reset. La diferencia es que si se activan ambas entradas se comportan como los biestables T, invirtiendo el valor de salida.
Bibliografía
Máquinas de estados finitos de Mealy y de Moore: electrositio.com.
Máquinas de estados finitos: techlib.net.
Circuitos secuenciales: www.dte.us.es.
Máquina de Mealy y máquina de Moore: barcelonageeks.com.
Biestables: Wikipedia.