Capítulo 6 - Modelado en 2D
Hasta este momento se ha visto varios ejemplos de programación gráfica implementando diferentes técnicas. A partir de ahora nos centraremos en generar nuestra imagen como un conjunto de objetos visuales. Crearemos un modelo para representar nuestra escena describiendo los objetos que la componen. Representaremos cada objeto en términos de su geometría y topología. La necesidad de colocar los objetos en la escena nos fuerza a describirlos según su posición. Nos basaremos en un sistema de coordenadas, como el plano cartesiano, para situar cada uno de estos objetos.
Para crear y manipular modelos para poder crear las escenas que compondrán nuestra imagen, necesitamos describir nuestros modelos y sus operaciones numérica y geométricamente. Esto supone usar las matemáticas para poder desarrollar las imágenes que nos interesan generar.
Conceptos
Para poder entender las operaciones y algoritmos que usaremos para modelar nuestros objetos y escenas, debemos comprender algunos conceptos matemáticos fundamentales.
Vamos a definir brevemente los conceptos acerca de tres tipos básicos de entidades para describir nuestros objetos y que nos proporcionarán ciertas propiedades importantes:
Escalares
Básicamente, se trata de números reales que tienen dos operaciones importantes: la suma y la multiplicación. También tienen las siguientes propiedades:
-
Conmutativa:
a + b = b + a a * b = b * a
-
Asociativa:
a + (b + c) = (a + b) + c a * (b * c) = (a * b) * c
-
Distributiva:
a * (b + c) = (a * b) + (a * c)
Existen dos escalares especiales: el elemento neutro 0 para la suma y el 1 para la multiplicación. Esto es,
a + 0 = 0 + a = a a * 1 = 1 * a = a
Además, existen las inversas de la suma, descrita como -a, y de la multiplicación, descrita como a-1. Esto es,
a + (-a) = 0 a * a-1 = 1
Puntos
Un punto no es nada más que una ubicación en un espacio sin siquiera tener tamaño. Los puntos existen irrelevantemente de un sistema de referencia o de coordenadas. Obviamente, sería inconveniente e impráctico describir cada punto existente sin usar un sistema de coordenadas.
Vectores
Geométricamente, un vector es un segmento orientado que tiene dirección, sentido (u orientación), y magnitud, representada como la longitud del segmento. Un vector no tiene posición, por lo que dos vectores son idénticos si tienen la misma dirección, orientación, y magnitud. Al igual que ocurre con los puntos, necesitaremos un sistema de coordenadas para referirnos a cualesquier vectores.
Nota: Sugerimos consultar el Apéndice 2 para profundizar en el tema de los vectores.
Espacios
Nos interesa hablar de ciertos espacios concretos, como son:
-
El espacio vectorial, o a veces llamado el espacio vectorial lineal, se compone de escalares y de vectores.
Se definen varias operaciones con estas entidades y entre sí.
Nota: Consulten el Apéndice 2 para más información acerca de estas operaciones.
- El espacio afín amplía el espacio vectorial agregando el concepto de puntos. Con estas entidades, podemos crear un sistema de coordenadas, descrito como una base de vectores y el punto de origen.
- El espacio euclidiano agrega al espacio afín la noción de distancia o la medida de tamaño. La nueva operación principal es el llamado producto interno que resulta en un escalar a partir de dos vectores. Por esta razón, se suele llamar producto escalar a esta operación.
Líneas
Una línea recta es un conjunto infinito de puntos que comparte una misma pendiente o dirección. Podemos describir cualquier punto en una línea con las entidades descritas anteriormente; esto es,
P(t) = P0 + t v
donde P0 es un punto arbitrario y conocido, t es un escalar, y v es un vector. P(t) describirá cualquier punto en la línea según el parámetro t.
Al ajustar un sistema de coordenadas, la fórmula de una línea recta, en dos dimensiones, se convierte en la siguiente:
(x(t),y(t)) = (x0,y0) + t (vx,vy)
Se puede convertir lo anterior en el siguiente sistema de ecuaciones:
x(t) = x0 + t vx y(t) = y0 + t vy
Despejando el parámetro t de este sistema de ecuaciones, obtenemos la siguiente fórmula más familiar:
(y(x)-y0) = m (x-x0)
donde m es la pendiente que es igual a vy/vx. Esta ecuación termina siendo el siguiente polinomio,
y(x) = m x + b
Convexidad
Un polígono es convexo si cada segmento que une cada dos de sus vértices existe completamente en el interior de tal polígono. También podemos decir que un polígono es convexo si el ángulo formado por cada pareja contigua de aristas queda comprendida entre 0° y 180° (ambos incluidos).
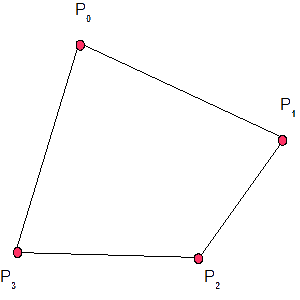
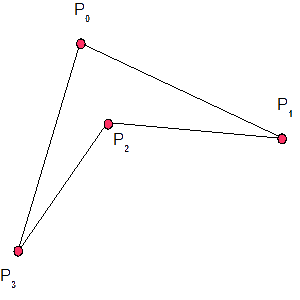
Ahora podemos continuar con otros conceptos que necesitamos para crear y controlar los modelos de los objetos gráficos. Los objetos que vamos a tratar por el momento serán compuestos por uno o varios polígonos convexos. Al manejar polígonos, podemos describirlos a través de un conjunto de vértices y aristas. Trabajar con polígonos, vértices, y aristas es más simple que manipular objetos más complejos basados en fórmulas y funciones matemáticas complicadas. Si usáramos objetos complejos, se nos complicaría bastante la generación de la imagen. En otros capítulos, veremos otras técnicas avanzadas para crear modelos más complicados pero más realistas. Por el momento, veremos las técnicas necesarias para generar y visualizar objetos basados en modelos que aproximen aquellos objetos más complicados.
Sistema de Coordenadas
Hemos visto los objetos abstractos: escalares, puntos, y vectores. Ahora asociaremos estos objetos a un sistema de coordenadas como referencia.
El sistema de coordenadas o sistema de referencia es un conjunto de N escalares para referirse unívocamente a cada punto en un espacio de N dimensiones. Por ejemplo, en dos dimensiones (2D), cada punto es descrito por dos escalares que representan dos coordenadas. El típico sistema de coordenadas que usamos es el llamado sistema de coordenadas cartesianas o rectangulares. Este sistema de coordenadas se basa en anchura y altura - las mismas propiedades de un rectángulo. También es usual usar el sistema de coordenadas polares, que se basa en un radio y en un ángulo, para describir cualquier punto.
Por el momento nos ceñiremos a usar un sistema de coordenadas rectangulares. Describimos este sistema a través de una base - conjunto de vectores linealmente independientes. Por ejemplo, podemos describir un vector cualquiera, q, de esta manera:
q = a u + b v
donde a y b son escalares y componentes de q, mientras que u y v son vectores que forman una base.
Una base involucra vectores, pero como los vectores no tienen posición, necesitamos un punto de referencia para nuestro sistema de coordenadas. Por ello, creamos un marco de referencia en espacios afines. Un marco de referencia se compone de la base que describe un sistema de coordenadas y un punto de referencia que describe el origen. De esta forma, fijamos los vectores de la base en un solo punto. Ahora podemos describir cualquier vector en un marco de la misma forma que en el espacio vectorial:
q = a u + b v

También podemos describir únicamente cualquier punto, P, en un marco, de esta manera:
P = O + a u + b v
donde O es el punto de origen.
Cambio de Coordenadas
Frecuentemente, querremos representar un punto o un vector en una base a su equivalente en otra base.
Esto supone cambiar de un sistema de coordenadas a otro.
Digamos que tenemos dos bases:
u1 = a11 v1 + a12 v2 u2 = a21 v1 + a22 v2
Describimos el conjunto de los componentes escalares como una matriz; esto es,
( a11 a12 )
M = ( a21 a22 )
Usando matrices, obtenemos la siguiente expresión,
( u1 ) ( a11 a12 ) ( v1 ) ( u2 ) = ( a21 a22 ) ( v2 )
Para poder cambiar la representación de
( v1 )
v = ( vx vy ) ( v2 )
Para representar v en la base de
( u1 )
u = ( ux uy ) ( u2 )
Para llevar a cabo la conversión, queremos averiguar los valores de
( u1 ) ( v1 )
( ux uy ) ( u2 ) = ( vx vy ) ( v2 )
Sustituimos la base
( a11 a12 ) ( v1 ) ( v1 )
( ux uy ) ( a21 a22 ) ( v2 ) = ( vx vy ) ( v2 )
Como la matriz de la base
( a11 a12 )
( ux uy ) ( a21 a22 ) = ( vx vy )
Como conocemos la matriz, M, y el vector, v, necesitamos despejar la matriz del lado izquierdo de la igualdad, para determinar los valores desconocidos que representa el vector, u. Esto es,
u M = v u M M-1 = v M-1 u I = v M-1 u = v M-1
La ecuación final es la siguiente, que se basa en calcular la inversa de la matriz, M,
( a11 a12 )-1
u = v ( a21 a22 )
Este cambio de bases no varía el origen y por tanto podemos usarlo para describir rotaciones y cambios de escala de una base en términos de otra base. Sin embargo, para realizar una traslación del origen o un cambio de marco, no se puede representar de esta forma. Antes de ver este cambio de marco, veamos un ejemplo de un cambio de coordenadas.
Nota: Aconsejamos ver el Apéndice 3 para una introducción a las matrices.
Ejemplo
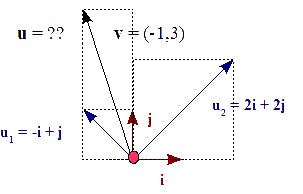
Tenemos el vector, v = ( -1, 3 ), en la base
v = -1 i + 3 j
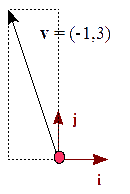
Ahora queremos representar v en la base
u1 = -1 i + 1 j u2 = 2 i + 2 j
Por lo tanto, la matriz de los componentes de los vectores es la siguiente:
( -1 1 )
M = ( 2 2 )
Para realizar el cambio de coordenadas, necesitamos calcular la inversa de M, que es,
( -1 1 )-1
M-1 = ( 2 2 ) = A
( -0,50 0,25 )
A = ( 0,50 0,25 )
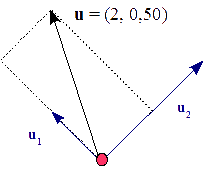
En la nueva representación, llamemos a v el vector, u, cuya representación es la siguiente:
u = v A
( -0,50 0,25 )
u = ( -1 3 ) ( 0,50 0,25 )
Coordenadas Homogéneas
Uno de los problemas con que nos enfrentamos es la posible confusión entre un punto y un vector, a la hora de representarlos.
Por ejemplo,
En el marco descrito por
P = a u1 + b u2 + P0
Podemos expresar lo anterior con matrices, resultando en lo siguiente:
( u1 )
P = ( a b 1 ) ( u2 )
( P0 )
Asimismo, podemos expresar cualquier vector del mismo marco de la siguiente manera:
v = c u1 + d u2
La expresión en forma matricial es la siguiente:
( u1 )
v = ( c d 0 ) ( u2 )
( P0 )
Podemos expresar este vector sencillamente como:
v = ( c d 0 )
Resumiendo, con las coordenadas homogéneas,
- Podemos representar y manipular puntos y vectores de la misma manera.
-
Cualquier punto en 2D se representará así,
P = ( x, y, 1 ) . -
Cualquier vector en 2D se representará así,
v = ( vx, vy, 0 ) .
Existe una relación lineal entre un punto en 2D y su representación en coordenadas homogéneas.
Al extender un punto en 2D a uno en 3D, éste se convierte en una línea recta de la forma,
Cambio de Marcos de Referencia
Usando coordenadas homogéneas, podemos realizar un cambio de marcos de referencia entre
u1 = a11 v1 + a12 v2 u2 = a21 v1 + a22 v2 Q0 = a31 v1 + a32 v2 + P0
En forma matricial, obtenemos la siguiente fórmula,
( u1 ) ( a11 a12 0 ) ( v1 ) ( u2 ) = ( a21 a22 0 ) ( v2 ) ( Q0 ) ( a31 a32 1 ) ( P0 )
La matriz de componentes escalares es la llamada matriz de representación del cambio de marcos de referencia. Se define de esta manera:
( a11 a12 0 )
M = ( a21 a22 0 )
( a31 a32 1 )
Podemos cambiar la representación de un punto o de un vector al tener diferentes marcos de referencia.
Si v es un vector descrito en el marco de
( v1 )
v = ( vx vy 0 ) ( v2 )
( P0 )
su representación, u, en el marco de
( u1 )
u = ( ux uy 0 ) ( u2 )
( Q0 )
Para calcular los escalares de
( a11 a12 0 )-1
u = v ( a21 a22 0 )
( a31 a32 1 )
Ejemplos de Cambio de Marcos
Veamos dos ejemplos de cambio de marcos de referencia.
-
Volvamos al ejemplo anterior:
Tenemos el vector, v = ( -1, 3, 0 ), en el marco
{i,j, (0,0)}, que se representa así:v = -1 i + 3 j
Ahora queremos representar v en el marco
{u1,u2, Q0} cuya representación es la siguiente, en términos de{i,j, (0,0)}: u1 = -1 i + 1 j u2 = 2 i + 2 j Q0 = 2 i - 1 j + (0,0)
La matriz de la representación es la siguiente,
( -1 1 0 ) M = ( 2 2 0 ) ( 2 -1 1 )La inversa de la matriz, M, es la siguiente matriz, A,
( -1 1 0 )-1 M-1 = ( 2 2 0 ) = A ( 2 -1 1 ) ( -0,50 0,25 0 ) A = ( 0,50 0,25 0 ) ( 1,50 -0,25 1 )El vector, v, representado en el nuevo marco se llamará u, que se define como,
( -0,50 0,25 0 ) u = ( -1 3 0 ) ( 0,50 0,25 0 ) = ( 2 0,50 0 ) ( 1,50 -0,25 1 )Como podemos observar, obtenemos el mismo resultado que en el ejemplo anterior, cuando hicimos un cambio de coordenadas. Esto es porque los vectores no tienen posición y por tanto el cambio del punto de origen no afecta a los vectores ni contribuye a su representación.
-
Veamos lo que sucede al representar el punto, P = ( 1, -1 ) en el marco
{i,j, (0,0)}: P = 1 i - 1 j + (0,0) = i - j
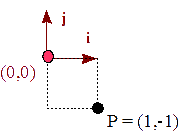
Figura 8 - Definición de P en el marco {i,j, (0,0)} Ahora queremos representar el punto, P, en el marco
{u1,u2, (2,-1)}. La matriz de representación de este marco es la siguiente:( -1 1 0 ) M = ( 2 2 0 ) ( 2 -1 1 )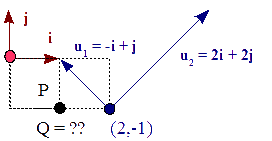
Figura 9 - Definiciones de P y el marco {u1,u2, (2,-1)} en el marco {i,j, (0,0)} La nueva representación del punto, P, se calcula de la siguiente manera:
Q = P M-1 ( -0,50 0,25 0 ) Q = ( 1 -1 1 ) ( 0,50 0,25 0 ) = ( 0,50 -0,25 1 ) ( 1,50 -0,25 1 )Se trata del mismo punto en el espacio euclidiano, pero según el marco de referencia, se puede representar de dos formas diferentes:
( 1, -1 ) ó( 0,50, -0,25 ). 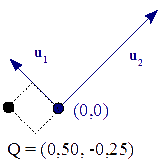
Figura 10 - Representación de P como Q en la base {u1,u2}
Transformaciones Afines
Una transformación es una función que acepta un punto y lo convierte - siguiendo alguna lógica o algoritmo - en otro punto. Asimismo se puede decir de una transformación de un vector a otro vector. Si usamos coordenadas homogéneas, podemos representar cualquier transformación usando la misma función para aceptar tanto puntos como vectores. El problema es que esta definición es demasiado general para nuestros propósitos. Como vamos a estar manejando objetos geométricos más complicados que puntos y vectores, sería impráctico aplicar la misma transformación a cada punto y vector que compone nuestros objetos en nuestra escena y en nuestra imagen.
Necesitamos limitar las transformaciones que queremos usar. La restricción más importante es la linealidad. Sin entrar en mucho detalle, el uso de transformaciones lineales supone que una línea se convierte en una línea. De esta manera, podemos transformar los puntos finales que describen un segmento para así transformar tal segmento, sin tener que transformar todos los puntos que comprenden tal segmento. Usando coordenadas homogéneas, tales transformaciones implicarán una multiplicación matricial. Podemos representar tal transformación entre a y b, que pueden representar tanto puntos como vectores, de esta manera,
a = b M
Como podemos ver, esta fórmula es idéntica a la que usamos para el cambio de marco de referencia. Por lo tanto, una transformación lineal corresponde a un cambio de marco. Dicho esto, declaramos que una transformación es a) un cambio de representación de los objetos de un marco de referencia a otro o b) un cambo de las figuras de los objetos dentro del mismo marco de referencia.
Volviendo a la matriz en coordenadas homogéneas,
( a11 a12 0 )
M = ( a21 a22 0 )
( a31 a32 1 )
vemos que sólo tenemos 6 elementos con los que trabajar de los 9 que existen en una matriz de 3x3. Técnicamente, decimos que esta matriz tiene 6 grados de libertad. Sin embargo, al aplicar este tipo de matrices para transformar un punto o un vector, podemos deducir dos tipos de matrices diferentes. Como un vector se define así,
v = ( vx vy 0 )
la transformación acaba siendo la siguiente matriz,
( a11 a12 0 )
Mvector = ( a21 a22 0 )
( 0 0 1 )
Como la coordenada homogénea de un vector es cero, los elementos a31 y a32 de la matriz no influyen en el resultado de la multiplicación.
Para transformar un punto, descrito como,
P = ( Px Py 1 )
la transformación es la siguiente matriz,
( a11 a12 0 )
Mpunto = ( a21 a22 0 )
( a31 a32 1 )
Por lo tanto, existen 4 grados de libertad para una transformación de vectores, pero usamos los 6 grados para las transformaciones afines con puntos.
Operaciones
Existen cuatro transformaciones afines: traslación, cambio de escala, rotación, y sesgado o transvección. Usando coordenadas homogéneas, cada transformación se puede representar como una matriz de 3x3 de la forma,
( a11 a12 0 )
M = ( a21 a22 0 )
( a31 a32 1 )
Traslación
Se trata de una operación que desplaza un punto una distancia fija en una dirección y sentido concretos.
El parámetro que se necesita es simplemente un vector a modo de desplazamiento:
P′ = P + d
donde,
P = ( Px Py 1 ) P′ = ( P′x P′y 1 ) d = ( dx dy 0 )
Podemos reescribir estas ecuaciones por componentes,
P′x = Px + dx P′y = Py + dy
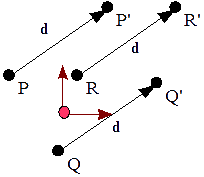
Como vemos, una traslación trata de una suma. Esto va en contra de la multiplicación matricial que hemos estado aplicando hasta estos momentos. Sin embargo, no tenemos un grave problema al usar coordenadas homogéneas,
P′ = P T
donde,
( 1 0 0 )
T = ( 0 1 0 )
( dx dy 1 )
Analizando esta matriz, vemos que tiene 2 grados de libertad.
Por ello, solemos describir una traslación como una función que acepta dos parámetros:
Como no podemos conseguir el mismo resultado con una matriz de 2x2, se usa una matriz de 3x3 y coordenadas homogéneas como una forma ingeniosa de convertir una suma a una multiplicación. Esto nos permitirá "encadenar" las transformaciones como multiplicaciones entre matrices. Con una suma de por medio, no podrímos hacer tal "encadenación", ya que las multiplicaciones se deben realizar antes de las sumas.
Podríamos calcular la inversa de la matriz de traslación con el algoritmo general. Sin embargo, para la traslación, existe una solución sencilla basada en la geometría. La inversa de una traslación es sencillamente otra traslación en el sentido contrario. Esto es,
( 1 0 0 )
T = ( 0 1 0 )
( dx dy 1 )
( 1 0 0 )
T-1 = ( 0 1 0 )
( -dx -dy 1 )
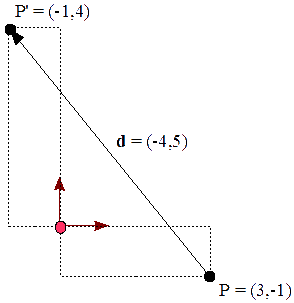
Veamos un ejemplo sencillo, desplazando un punto,
P′ = P T(-4,5)
( 1 0 0 )
( P′x P′y 1 ) = ( 3 -1 1 ) ( 0 1 0 )
( -4 5 1 )
P′ = ( -1 4 1 )
Cambio de Escala
Esta operación sirve para modificar proporcional, pero no necesariamente uniformemente, los valores que representan los puntos o vectores a través de dos factores; uno para cada dimensión. Este factor multiplica cada valor de la entidad - punto o vector - en cuestión aumentando o reduciendo tal valor. Al aplicar esta operación a un objeto compuesto por segmentos, el resultado visual será el de un cambio de tamaño. Algebraicamente, expresamos esta operación de la siguiente manera:
P′x = Px * sx P′y = Py * sy
donde, P contiene las coordenadas del punto original, P′ las del punto transformado, y sx y sy son los factores para el cambio de escala:
P = ( Px Py 1 ) P′ = ( P′x P′y 1 )
En forma matricial, obtenemos la siguiente fórmula:
P′ = P S
donde,
( sx 0 0 )
S = ( 0 sy 0 )
( 0 0 1 )
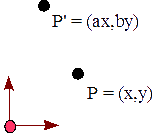
Como ocurre con la matriz de traslación, la matriz para el cambio de escala también tiene 2 grados de libertad.
Asimismo podemos representar esta operación como una función que acepta dos parámetros:
Además de agrandar y reducir el tamaño, podemos crear el efecto de reflejo al usar números negativos. También hay que tener en cuenta que al multiplicar por un punto, éste puede cambiar de posición. Como esto no ocurre con el origen, (0,0), podemos multiplicar cualquier factor por este punto, sin variarlo. Por lo tanto, se suele elegir el origen para fijar un punto al aplicar un cambio de escala.
La inversa de una matriz de cambio de escala es simplemente la inversa de la multiplicación: la división. Esto es,
( sx 0 0 )
S = ( 0 sy 0 )
( 0 0 1 )
( 1/sx 0 0 )
S-1 = ( 0 1/sy 0 )
( 0 0 1 )
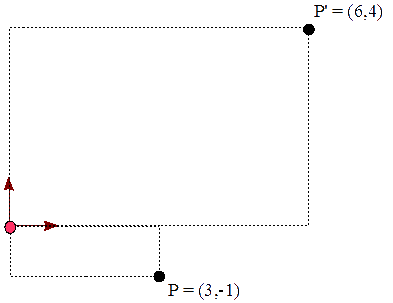
Ejemplo
Veamos un ejemplo, para aumentar y aplicar reflejo al siguiente punto,
P′ = P S(2,-4)
( 2 0 0 )
( P′x P′y 1 ) = ( 3 -1 1 ) ( 0 -4 0 )
( 0 0 1 )
P′ = ( 6 4 1 )
Rotación
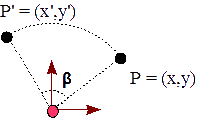
En esta operación, el punto es transformado siguiendo el camino de una circunferencia con el origen como su centro. El camino a recorrer depende del ángulo indicado. Las siguientes ecuaciones describen esta operación usando forma polar,
Px = r * cos α Py = r * sen α P′x = r * cos( α + β ) P′y = r * sen( α + β )
donde, P es el punto original, P′ el punto transformado, r es el radio en forma polar, y α y β son los ángulos inicial y final, respectivamente:
P = ( Px Py 1 ) P′ = ( P′x P′y 1 )
Usando identidades trigonométricas, sustituimos los cosenos y senos de una suma de ángulos por expresiones equivalentes. Obtenemos la siguiente ecuación,
P′x = r * cos α cos β - r * sen α sen β P′y = r * sen α cos β + r * cos α sen β
Aplicando las definiciones anteriores a estas ecuaciones, obtenemos que,
P′x = Px cos β - Py sen β = Px cos β - Py sen β P′y = Py cos β + Px sen β = Px sen β + Py cos β
En forma matricial, obtenemos la siguiente fórmula:
P′ = P R
donde,
( cos β sen β 0 )
R = ( -sen β cos β 0 )
( 0 0 1 )
Esta matriz de rotación supone 4 grados de libertad y sólo requiere un parámetro: el ángulo de rotación.
El ángulo se interpreta como positivo en el sentido contrario de las agujas del reloj a partir del eje X del marco de referencia.
Podemos definir la rotación como una función, escribiendo:
La inversa de una rotación es sencillamente otra rotación con el mismo ángulo pero negativo, para indicar un sentido contrario del ángulo original. Esto es,
( cos β sen β 0 )
R = ( -sen β cos β 0 )
( 0 0 1 )
( cos -β sen -β 0 ) ( cos β -sen β 0 )
R-1 = ( -sen -β cos -β 0 ) = ( sen β cos β 0 )
( 0 0 1 ) ( 0 0 1 )
Ejemplo
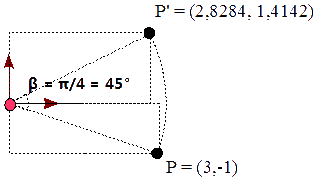
Veamos un ejemplo para rotar el siguiente punto,
P′ = P R(π/4)
( cos π/4 sen π/4 0 )
( P′x P′y 1 ) = ( 3 -1 1 ) ( -sen π/4 cos π/4 0 )
( 0 0 1 )
( √2/2 √2/2 0 )
P′ = ( 3 -1 1 ) ( -√2/2 √2/2 0 )
( 0 0 1 )
P′ = ( 2,8284 1,4142 1 )
Sesgado
La transvección o el sesgado trata de mudar todas las entidades en la misma dirección a lo largo de un eje. Esta combinación de traslación y cambio de escala "deforma" las entidades, tirando de ellas en ambos sentidos en la misma dirección. La deformación se basa en el ángulo, α, formado por el eje elegido y la línea que corta el eje elegido y contiene los nuevos puntos transformados. Las ecuaciones que describen esta operación a lo largo del eje X son las siguientes,
P′x = Px + Py cotg α P′y = Py
donde,
P = ( Px Py 1 ) P′ = ( P′x P′y 1 )
Esto nos lleva a la siguiente forma matricial,
P′ = P Hx
donde,
( 1 0 0 )
Hx = ( cotg α 1 0 )
( 0 0 1 )
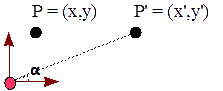
Podemos observar perfectamente que esta matriz sólo tiene 1 grado de libertad.
Debemos tener cuidado con los valores de α, ya que la cotangente puede dispararse hacia el infinito,
si el ángulo es 0 ó π (180°).
La restricción para el ángulo es la siguiente:
Realizar la operación inversa de un sesgado supone otro sesgado con el mismo ángulo en forma negativa. Esto es,
( 1 0 0 )
Hx = ( cotg α 1 0 )
( 0 0 1 )
( 1 0 0 ) ( 1 0 0 )
Hx-1 = ( cotg -α 1 0 ) = ( -cotg α 1 0 )
( 0 0 1 ) ( 0 0 1 )
Para conseguir la matriz para el sesgado a lo largo del eje Y, derivamos las ecuaciones de una manera muy parecida:
P′x = Px P′y = Px cotg α + Py
Obtendríamos la siguiente matriz,
( 1 cotg α 0 )
Hy = ( 0 1 0 )
( 0 0 1 )
Ejemplo
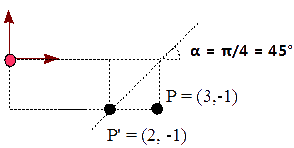
Veamos un ejemplo sesgando el punto,
P′ = P Hx(π/4)
( 1 0 0 )
( P′x P′y 1 ) = ( 3 -1 1 ) ( cotg π/4 1 0 )
( 0 0 1 )
( 1 0 0 )
P′ = ( 3 -1 1 ) ( 1 1 0 )
( 0 0 1 )
P′ = ( 2 -1 1 )
Uso de Transformaciones
Las transformaciones básicas que se han visto hasta ahora controlan las entidades - puntos y vectores - que operan, con resultados diferentes. Analizando estas transformaciones, podemos clasificarlas según el efecto, que provocan, de las entidades resultantes. Se suele hablar de transformaciones de "cuerpo rígido", que son aquellas transforamciones cuyos cuerpos no sufren deformaciones. Cualquier secuencia de traslaciones y rotaciones cumple con este criterio, ya que no distorsiona el objeto, conservando el paralelismo y las longitudes de las líneas al igual que los ángulos. Sin embargo, operaciones que incluyan cambios de escala y sesgados moldean los cuerpos, por lo que no conservan las longitudes de las líneas ni los ángulos. Aun existiendo estas diferencias, sí podemos garantizar que cualquier transformación afín conserva el paralelismo de las líneas.
Con estas transformaciones, podemos crear nuevas operaciones compuestas por las operaciones básicas. Para llevar a cabo esta composición, aplicamos una serie de transformaciones multiplicándolas por cada entidad a transformar. Multiplicamos la matriz, que representa la transformación, por el punto o vector. Esto es,
P′ ← P M0 P′ ← P′ M1 P′ ← P′ M2 P′ ← P′ M3 P′ ← P′ M4 . . . P′ ← P′ Mn
Como se trata de multiplicaciones de varias transformaciones, Mn, aplicadas a los mismos puntos original y transformados, P, podemos agrupar estas matrices de transformaciones en una serie de multiplicaciones. Esto es,
P ← P M0 M1 M2 … Mn
Podemos agregar más matrices al producto para aplicar más transformaciones, creando una encadenación. Al multiplicar todas las matrices de transformación, terminaremos con una sola matriz que recoge todas las transformaciones aplicadas a la entidad en cuestión. De esta manera, podemos multiplicar varias matrices iguales para luego multiplicar la transformación resultante a todas las entidades que nos interesan. Esto optimiza la cantidad de multiplicaciones que debemos hacer. Por ejemplo,
M ← M0 M1 M2 … Mn P′0 ← P0 M P′1 ← P1 M P′2 ← P2 M P′3 ← P3 M . . . P′n ← Pn M
Composición
Veamos algunas transformaciones compuestas que nos pueden ser útiles en el manejo de nuestros modelos 2D.
Debemos tener presente que una secuencia de transformaciones no es necesariamente igual a la misma secuencia en diferente orden.
Por ejemplo, la secuencia
El primer ejemplo que trataremos es rotar un objeto por un punto fijo. Como ya hemos explicado, la rotación se realiza por el origen (0,0). Para rotar por otro punto, simplemente mudamos ese punto fijo al origen, rotamos por el origen, y luego devolvemos el punto a las coordenadas del punto fijo. Algebraicamente, representamos esta idea de la siguiente manera:
M = T(-pf) R(α) T(pf)
donde,
Podemos multiplicar todas las matrices para obtener la matriz resultante, M, que es la siguiente:
( cos α sen α 0 )
M = ( -sen α cos α 0 )
( (xf - xf cos α + yf sen α) (yf - xf sen α - yf cos α) 1 )
Ejemplos
Veamos unos ejemplos prácticos.
-
Tenemos dos puntos,
p = (4,2) yq = (-3,1). Queremos rotar estos dos puntos alrededor del punto (fijo),F = (2,-1), por un ángulo,α = π/6 (30°), p′ = p T( (-2,1) ) R(π/6) T( (2,-1) ) q′ = q T( (-2,1) ) R(π/6) T( (2,-1) )
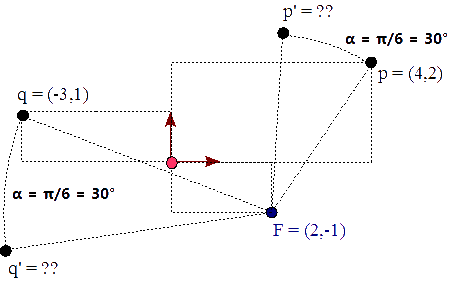
Figura 19 - Rotación de los puntos p y q por el punto F con ángulo α Calculemos la matriz resultante, M,
( cos π/6 sen π/6 0 ) M = ( -sen π/6 cos π/6 0 ) ( (2 - 2 cos π/6 - sen π/6) (-1 - 2 sen π/6 + cos π/6) 1 )Aplicando la matriz resultante, obtenemos el siguiente paso,
( 0,8660 0,5 0 ) p′ = ( 4 2 1 ) ( -0,5 0,8660 0 ) ( -0,2321 -1,1340 1 ) ( 0,8660 0,5 0 ) q′ = ( -3 1 1 ) ( -0,5 0,8660 0 ) ( -0,2321 -1,1340 1 )Los resultados son los siguientes,
p′ = ( 2,2321, 2,5981 ) q′ = ( -3,3301, -1,7680 )
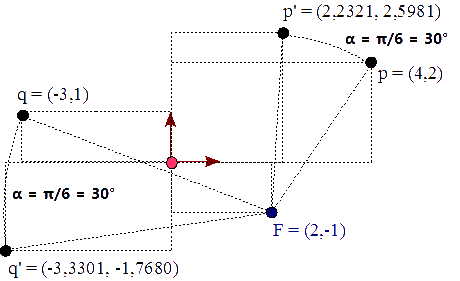
Figura 20 - Los puntos p′ y q′ -
Otro ejemplo parecido al anterior es a la hora de agrandar o empequeñecer un objeto el cual está compuesto por varios puntos y líneas. Esto supone un cambiar de escala, pero como hemos visto anteriormente, esta operación también realiza una traslación proporcional a los parámetros del cambio de escala. La solución es mudar el objeto al origen, realizar la operación del cambio de escala, para luego regresar el mismo objeto a su posición original. Esto supone que debemos elegir un punto fijo e invariable para poder trasladar y fijar el objeto al origen. Veamos las operaciones matriciales básicas para implementar esta operación compleja:
M = T(-pf) S(sx,sy) T(pf)
donde,
pf = (xf,yf) es el punto fijo por el que queremos cambiar el tamaño de cualquier entidad según los factores indicados porsx ysy. Multiplicando todas estas matrices obtenemos la siguiente matriz resultante, M,
( sx 0 0 ) M = ( 0 sy 0 ) ( xf(1 - sx) yf(1 - sy) 1 ) -
Veamos un ejemplo de esta transformación.
Tenemos un cuadrilátero formado por cuatro puntos,
p = (4,2), q = (-3,1), r = (-2,-2), ys = (3,0). Vamos a agrandar este objeto desproporcionalmente: sx = 2 y sx = 0,5 y fijado en el punto,F = (1,2). Algebraicamente, tenemos lo siguiente,p′ = p T( (-1,-2) ) S(2, 0,5) T( (1,2) ) q′ = q T( (-1,-2) ) S(2, 0,5) T( (1,2) ) r′ = r T( (-1,-2) ) S(2, 0,5) T( (1,2) ) s′ = s T( (-1,-2) ) S(2, 0,5) T( (1,2) )
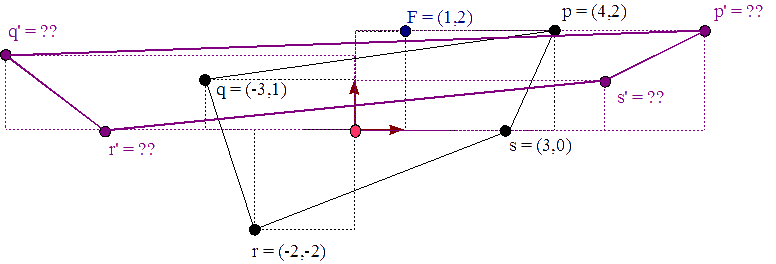
Figura 21 - Agrandamos desproporcionalmente un cuadrilátero fijado en F=(1,2) Calculemos la matriz resultante, M,
( 2 0 0 ) M = ( 0 0,5 0 ) ( -1 1 1 )Ahora multiplicamos cada punto, que describe nuestro objeto, por la matriz resultante,
( 2 0 0 ) p′ = ( 4 2 1 ) ( 0 0,5 0 ) ( -1 1 1 ) ( 2 0 0 ) q′ = ( -3 1 1 ) ( 0 0,5 0 ) ( -1 1 1 ) ( 2 0 0 ) r′ = ( -2 -2 1 ) ( 0 0,5 0 ) ( -1 1 1 ) ( 2 0 0 ) s′ = ( 3 0 1 ) ( 0 0,5 0 ) ( -1 1 1 )Al final, obtenemos la siguiente información,
p′ = ( 7, 2 ) q′ = ( -7, 1,5 ) r′ = ( -5, 0 ) s′ = ( 5, 1 )
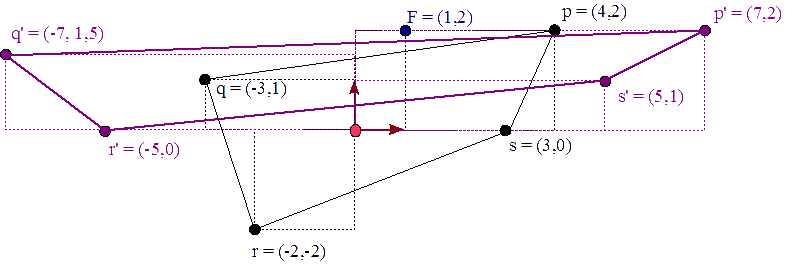
Figura 22 - El nuevo cuadrilátero formado por los puntos p′, q′, r′, y s′
Instancia
Otro claro ejemplo del uso de las transformaciones tiene que ver con la creación de nuevos objetos. En muchas ocasiones, queremos mostrar varios objetos basados en una misma figura. Sería algo engorroso describir las coordenadas exactas que describen cada instancia basada en la misma figura. Por ello, definimos un juego de diferentes objetos para luego crear cada objeto escogido de nuestro juego, que queremos mostrar en nuestra escena. Usando traslaciones, podemos colocar todas las instancias de cualesquier objetos en nuestra escena los cuales pueden estar descritos de una sola manera. Por supuesto, también podemos modificar cada instancia antes de colocarla en la escena. Esto supone aplicar otras transformaciones a nuestros objetos antes de trasladarlos a sus respectivas posiciones finales.
Ejemplo
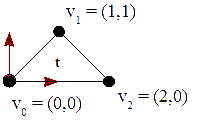
Describimos un triángulo, t, con la siguiente lista de vértices:
t0 = t S(-1,2) R(π/6) T( (3,4) ) t1 = t R(-π/6) Hx(π/12) T( (1,-6) ) t2 = t Hx(π/6) Hy(π/3) S(0,25, 2) T( (-5,0) ) t3 = t S(-1,-0,2) T( (-3,-2) )
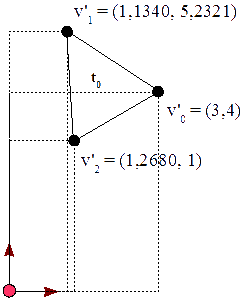
Las matrices resultantes para cada serie de transformaciones son las siguientes:
( -0,8660 -0,5 0 )
M0 = ( -1 1,7321 0 )
( 3 4 1 )
( -1 -0,5 0 )
M1 = ( 3,7321 0,8660 0 )
( 1 -6 1 )
( 0,25 1,1547 0 )
M2 = ( 0,4330 4 0 )
( -5 0 1 )
( -0,125 0 0 )
M3 = ( 0 -0,2 0 )
( -6 -5 1 )
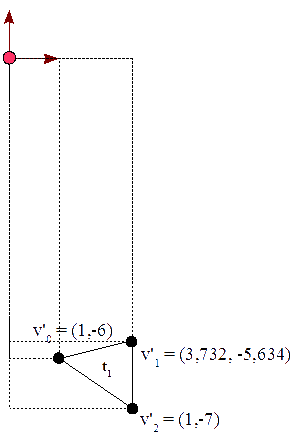
Acabaremos con los siguientes cálculos:
t0:v0 = ( 0 0 1 ) M0 t0:v1 = ( 1 1 1 ) M0 t0:v2 = ( 2 0 1 ) M0 t1:v0 = ( 0 0 1 ) M1 t1:v1 = ( 1 1 1 ) M1 t1:v2 = ( 2 0 1 ) M1 t2:v0 = ( 0 0 1 ) M2 t2:v1 = ( 1 1 1 ) M2 t2:v2 = ( 2 0 1 ) M2 t3:v0 = ( 0 0 1 ) M3 t3:v1 = ( 1 1 1 ) M3 t3:v2 = ( 2 0 1 ) M3
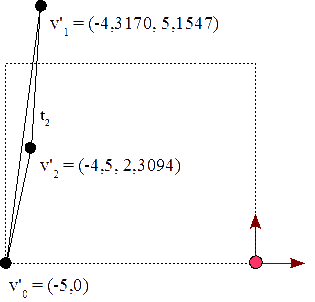
Como se puede ver, debemos aplicar las transformaciones a todos los puntos que representan los vértices de cada triángulo. Al final, obtendremos la siguiente información para los cuatro triángulos:
t0:v0 = ( 3 4 1 ) t0:v1 = ( 1,1340 5,2321 1 ) t0:v2 = ( 1,2680 3 1 ) t1:v0 = ( 1 -6 1 ) t1:v1 = ( 3,7321 -5,634 1 ) t1:v2 = ( 1 -7 1 ) t2:v0 = ( -5 0 1 ) t2:v1 = ( -4,3170 5,1547 1 ) t2:v2 = ( -4,5 2,3094 1 ) t3:v0 = ( -3 -2 1 ) t3:v1 = ( -4 -2,2 1 ) t3:v2 = ( -5 -2 1 )
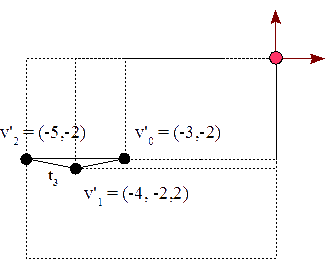
Modelado
Hasta ahora hemos visto la aplicación de las transformaciones afines a puntos. Sin embargo, nuestras escenas seguramente no se compondrán de puntos individuales, sino de objetos compuestos de segmentos. Asimismo, estos segmentos se compondrán de puntos. Como no podemos manipular todos los puntos individualmente en la práctica, sí podemos manipular los puntos finales del segmento. Por lo tanto, describiremos nuestros objetos según los puntos y los segmentos conectados entre ellos.
Representación
Para describir cada objeto, necesitaremos una forma de organizar la información: los puntos y segmentos. Además, capturaremos la geometría - puntos y segmentos - y la topología: la asociación de los puntos para formar la figura. Si pensamos jerárquicamente, daremos con la idea de descomponer un objeto geométrico en otros objetos más pequeños y fundamentales. Estos objetos fundamentales pueden ser representados como polígonos. Cada polígono a su vez se forma de vértices y aristas. Para describir las aristas de un polígono, crearemos una lista de vértices. De esta manera, optimizamos la cantidad de vértices que usaremos. Como seguramente tendremos polígonos que coincidan en una o varias aristas de otros polígonos, entonces también existirán vértices que coinciden. Por ello, es óptimo guardar una copia de cada vértice y luego referirnos a cada uno, en lugar de copiarlos. Podemos ver esta estrategia en el siguiente esquema acerca de la organización jerárquica de la información que describe un molino.
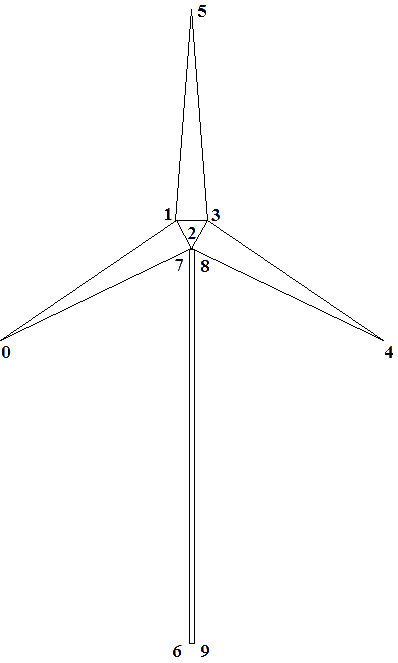
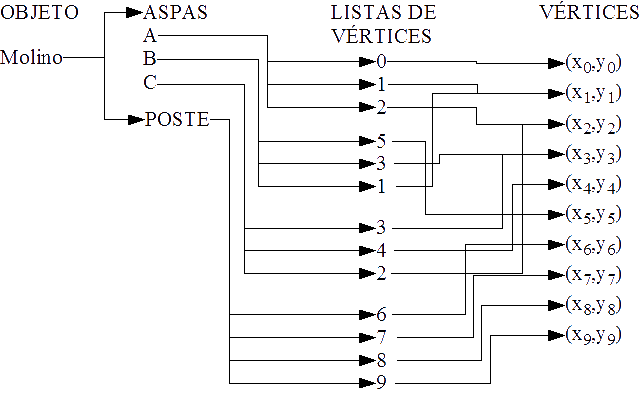
Un matiz importante a notar es el orden de los vértices para representar cada polígono. Hemos escogido los vértices contiguos en el sentido de las agujas del reloj. Esta elección se suele llamar operaciones de mano izquierda, porque podemos usar los cuatro dedos de la mano izquierda para seguir las aristas de un polígono. Este método tiene que ver con la representación que hemos hecho hasta estos momentos al igual que el álgebra matricial usada. Esto también tiene importancia cuando pasemos al modelado en 3D.
Orden de la Representación
Tenemos dos formas de representar la información en las matrices y vectores. Los elementos de cada fila pueden representar los valores para las coordenadas de los ejes X e Y. Por otro lado, también podríamos guardar las coordenadas en las columnas. Esto supondría cambiar el orden de las multiplicaciones matriciales. Típicamente, hablamos de operaciones matriciales de fila, con los elementos en cada fila, y las de columna, donde la información se guarda en las columnas.
Dependiendo del tipo de las operaciones matriciales, también nos interesa hablar de la manera de organizar la información de nuestros modelos. Geométricamente, tenemos que elegir los ejes y la relación entre ellos. Esta elección dictará la colocación y orientación de nuestros objetos geométricos. También definirá el sentido de las rotaciones. Por ello, solemos hablar de la regla de la mano derecha o de la mano izquierda. Esto hace alusión al uso de una mano u otra para determinar la relación entre los ejes y principalmente para las rotaciones. Como en dos dimensiones sólo tenemos dos ejes, no hablaremos de esta regla ya que sólo existe una orientación positiva sobre los ejes. Volveremos a tratar este concepto cuando veamos el modelado en tres dimensiones.
Hasta ahora y en el resto de este curso, usaremos las operaciones matriciales de fila y la regla de la mano izquierda.
Vista
Después de todas las transformaciones, que nos interesan aplicar a los objetos en nuestra escena, tenemos que convertir nuestra escena al medio que queremos. Nuestra escena se compone de los objetos geométricos. Sin embargo, la parte que queremos ver - la vista - se basa en un área que envuelve estos objetos geométricos de la escena. Típicamente, querremos mostrar la vista, como un área rectangular, en toda la pantalla, en píxeles. Por supuesto, existirán ocasiones en las que elegiremos una parte de la pantalla que contendrá nuestra vista. El paso de nuestro mundo o universo en 2D a la pantalla en 2D no es uno complicado, pero sí es necesario.
Podemos afrontar este problema como un cambio de representación.
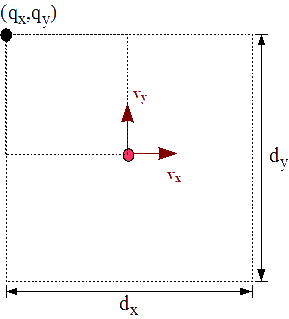
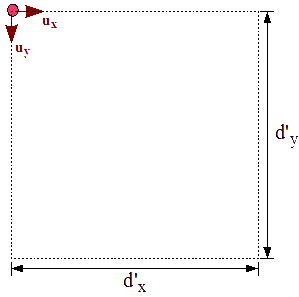
Tenemos el marco de referencia de nuestro universo descrito como
ux = sx vx uy = -sy vy Q0 = qx vx + qy vy
donde,
sx es el factor para el cambio de escala en el eje X; es decir, la proporción de anchuras de la escena y de la pantalla: dx/d′x
sy es el factor para el cambio de escala en el eje Y; es decir, la proporción de anchuras de la escena y de la pantalla: dy/d′y
(qx,qy) es el punto en la esquina superior izquierda que encuaderna nuestra escena. Este punto representará el origen en la pantalla.
La matriz de representación es la siguiente,
( sx 0 0 )
M = ( 0 -sy 0 )
( qx qy 1 )
Como queremos cambiar la representación, necesitaremos determinar la inversa de M, que es,
( 1/sx 0 0 )
M-1 = ( 0 -1/sy 0 )
( -qx/sx qy/sy 1 )
Ejemplo
Tenemos dos triángulos, s y t, en nuestra escena.
El marco de referencia que representa nuestro universo es el siguiente:
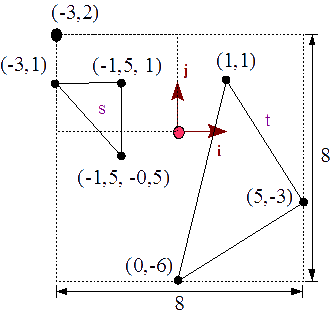
Queremos representar estos dos triángulos en la pantalla cuya resolución es
400 ux = 8 i 400 uy = -8 j Q0 = -3 i + 2 j
Simplificando, terminamos con,
ux = 0,02 i uy = -0,02 j Q0 = -3 i + 2 j
Obtenemos la siguiente matriz de representación,
( 0,02 0 0 )
M = ( 0 -0,02 0 )
( -3 2 1 )
Para poder cambiar la representación, necesitamos calcular la inversa de la matriz, M, que es,
( 50 0 0 )
M-1 = ( 0 -50 0 )
( 150 100 1 )
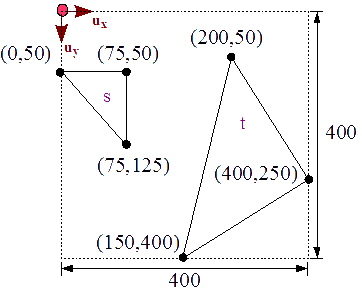
Podemos ver el resultado del cambio de representación de los vértices de ambos triángulos en la figura 33.
Otra forma de resolver el problema de conversión es aplicar una transformación compuesta de una traslación seguida de un cambio de escala. Trasladamos el punto en la esquina superior izquierda que de nuestra vista al origen. Luego, cambiamos de escala y con reflejo. Los factores de tal cambio de escala se basan en las proporciones de la anchura de la pantalla con respecto a la anchura de la vista para el eje X, y las proporciones de la altura de la pantalla con respecto a la altura de la vista para el eje Y. En forma matricial, tenemos la siguiente transformación afín,
M = T(-qx,-qy) S(sx,-sy)
donde,
sx es la proporción de las anchuras de la pantalla y de la escena: d′x/dx
sy es la proporción de las alturas de la pantalla y de la escena: d′y/dy
(qx,qy) es el punto que representará el origen en la pantalla de la esquina superior izquierda
del rectángulo que encuaderna nuestra escena.
Usando el ejemplo anterior, obtendríamos la siguiente matriz,
M = T(3,-2) S(400/8,-400/8)
Al final, conseguimos la misma matriz que la solución obtenida previamente al realizar un cambio de marco de referencia,
( 50 0 0 )
M-1 = ( 0 -50 0 )
( 150 100 1 )
Observaciones
La primera pregunta, que muchos iniciados se hacen, es "¿de verdad necesitamos hacer todo esto?". Aunque todos estos conceptos y la mecánica presentada parezcan más complicados de lo que deberían ser, nos servirán cuando pasemos a manipular y operar con objetos en tres dimensiones. Por ahora, todas estas operaciones nos servirán de base. Esto no significa que no deberíamos usar estas operaciones en dos dimensiones, especialmente cuando tenemos objetos complicados.
En la práctica, todas estas operaciones matriciales y vectoriales ya vienen implementadas en software como bibliotecas y API's gráficas y en hardware como instrucciones de la GPU (unidad de procesamiento gráfico) de las tarjetas aceleradoras gráficas. Tanto a nivel de hardware como de software, seguimos una arquitectura de procesamiento en serie y por etapas para generar una imagen a partir de su representación geométrica. Empezamos con la geometría de los objetos, que principalmente es el grupo de vértices. El procesamiento total de estos datos geométricos se puede repartir y distribuir por etapas o fases. En estos momentos, tenemos el siguiente esquema de distribución de tareas.

Los vértices pasan a ser transformados, según la lógica de nuestra aplicación. Estos vértices transformados son convertidos a nuestra superficie de dibujo, que puede representar nuestra pantalla, impresora, o en memoria. Por último, convertiremos las unidades de nuestra superficie de dibujo a píxeles o puntos de impresión. Esto supone convertir nuestra escena vectorial o continua en nuestra imagen final y discreta en píxeles en la pantalla o como puntos de impresión.
Iremos agregando más etapas a nuestro procesamiento a medida que vayamos viendo más técnicas. Asimismo, cuando pasemos al modelado en tres dimensiones, agregaremos a nuestro procesamiento algunas etapas relacionadas con el modelado en tres dimensiones.
Referencia
| Operación | Matriz | Inversa |
|---|---|---|
| Traslación: T(dx,dy) |
( 1 0 0 )
T = ( 0 1 0 )
( dx dy 1 )
|
( 1 0 0 )
T-1 = ( 0 1 0 )
( -dx -dy 1 )
|
| Cambio de escala: S(sx,sy) |
( sx 0 0 )
S = ( 0 sy 0 )
( 0 0 1 )
|
( 1/sx 0 0 )
S-1 = ( 0 1/sy 0 )
( 0 0 1 )
|
| Rotación: R(α) |
( cos α sen α 0 )
R = ( -sen α cos α 0 )
( 0 0 1 )
|
( cos α -sen α 0 )
R-1 = ( sen α cos α 0 )
( 0 0 1 )
|
| Sesgado en la X: Hx(α) |
( 1 0 0 )
Hx = ( cotg α 1 0 )
( 0 0 1 )
|
( 1 0 0 )
Hx-1 = ( -cotg α 1 0 )
( 0 0 1 )
|
| Sesgado en la Y: Hy(α) |
( 1 cotg α 0 )
Hy = ( 0 1 0 )
( 0 0 1 )
|
( 1 -cotg α 0 )
Hy-1 = ( 0 1 0 )
( 0 0 1 )
|
Ejercicios
Enlace al paquete de este capítulo.

-
Implemente una biblioteca para representar los puntos, vectores, y matrices al igual que sus operaciones, como pueden ser:
- suma
- resta
- producto escalar
- producto vectorial
- módulo, para calcular la magnitud (o distancia) de un vector
- normalizar un vector
- calcular el ángulo entre dos vectores
- determinante
- inversa
- traspuesta
Puede limitar la implementación de estas entidades y operaciones para representarlas y trabajar en coordenadas homogéneas.
Ejercicio 3 - Velero -
Implemente las transformaciones afines, en coordenadas homogéneas: traslación, cambio de escala, rotación, y sesgado. Estas operaciones realmente construyen las matrices que luego serán multiplicadas.
-
Dibuje una figura compuesta que más le guste. Por ejemplo, puede modelar y dibujar la siguiente imagen de un velero, compuesto por un casco, un mástil, y dos velas.
-
Redibuje el ejemplo presentado en el curso del molino moderno en la figura 28 para que use unas aspas antiguas. Por ejemplo,
Es una buena idea modelar un aspa y luego crear cuatro instancias para ser situadas en sus lugares correctos para crear las cuatro aspas del molino.