28 Objetos básicos del GDI:
Espacios de coordenadas y transformaciones
Definiciones
Un sistema de coordenadas es una representación del espacio plano basado en un sistema Cartesiano. Es decir, dos ejes perpendiculares.
En Windows, el espacio es limitado, es decir, el valor máximo de las coordenadas está acotado.
En Windows se usan cuatro sistemas de coordenadas:
- El del mundo. Se refiere al espacio de la aplicación. Permite usar 232 unidades en cada eje.
- El de la página. Es lo que normalmente denominamos espacio lógico, es decir, el espacio donde se usan las unidades lógicas, aunque también en el espacio del mundo trabajaremos con unidades lógicas. Permite usar 232 unidades en cada eje.
- El del dispositivo. En este espacio podemos trabajar con unidades como pulgadas o milímetros. Permite usar 227 unidades en cada eje.
- El del dispositivo físico. Generalmente se refiere al área de cliente, aunque también puede tratarse de la página de la impresora o del ploter. Su tamaño es variable, y depende de cada dispositivo.
Las transformaciones son algoritmos que se usan para hacer conversiones entre el espacio de coordenadas del mundo y el de la página, de modo que nos es posible realizar cambios de escala, rotaciones, traslaciones, deformaciones o reflexiones.
Esta característica se introdujo en el API de Win32, y no está disponible para versiones de Windows 95 y anteriores.
En Windows usaremos también otro tipos de proyecciones de coordenadas: el mapeo. El mapeo consiste en una transformación, aunque algo más limitada, ya que sólo permite escalar, trasladar y cambiar la orientación de los ejes.
El mapeo se aplica entre el espacio de página y el de dispositivo, y existe desde la creación de Windows. Nos permite trabajar con unidades físicas, como pulgadas o milímetros, y usar la orientación del espacio de la pantalla o el papel, en el que las y crecen hacia abajo, o la orientación matemática tradicional, en el que las y crecen hacia arriba.
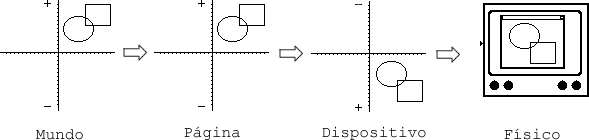
Espacios de coordenadas
Transformaciones
Ya hemos mencionado que las transformaciones y el espacio de coordenadas del mundo son elementos nuevos dentro del API de Win32. De modo que estas características no funcionan con versiones previas a Windosw NT, ni siquiera con Windows 95.
Las transformaciones usan un par de fórmulas sencillas para realizar el cambio de coordenadas del espacio del mundo al espacio de página. Si (x,y) son las coordenadas en el espacio del mundo, y (x',y') son las coordenadas en el espacio de página, las fórmulas para obtener estas coordenadas son:
x' = x * eM11 + y * eM21 + eDx y' = x * eM12 + y * eM22 + eDy
Estas fórmulas se pueden expresar mediante cálculo matricial:
| eM11 eM12 0 |
|x' y' 1| = |x y 1| · | eM21 eM22 0 |
| eDx eDy 1 |
La tercera matriz es la matriz de transformación. Esta matriz se maneja en el API mediante una estructura XFORM, y como los valores de la tercera columna son conocidos, no se guardan.
Si no modificamos la matriz de transformación, el sistema usa una matriz identidad, en la que todos los elementos son nulos, excepto la diagonal principal:
| 1 0 0 | | 0 1 0 | | 0 0 1 |
Si aplicamos esta matriz de transformación, no se produce ninguna transformación:
x' = x * eM11 + y * eM21 + eDx = x*1 + y*0 + 0 = x y' = x * eM12 + y * eM22 + eDy = x*0 + y*0 + 0 = y
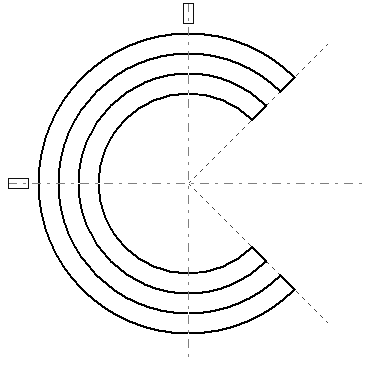
Traslaciones
Si analizamos cada término, veremos que eDx y eDy nos permiten hacer traslaciones, es decir, mover puntos en cualquier dirección. (eDx,eDy) es, sencillamente, un desplazamiento.
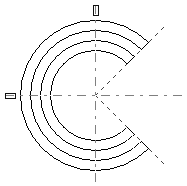
Cambio de escala
Si los términos eM21 y eM12 son nulos, podemos ver que eM11 y eM22 realizan un cambio de escala.
| 0.5 0 0 | | 0 0.5 0 | | 0 0 1 |
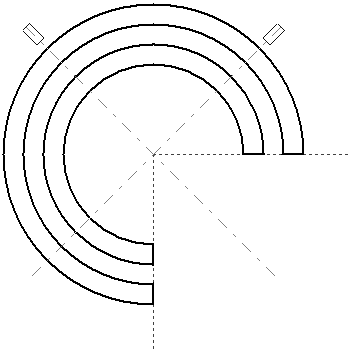
Rotaciones
Las rotaciones implican algunos cálculos trigonométricos sencillos, para rotar la figura un ángulo α, se aplica la siguiente fórmula:
x' = x * cos(α) + y * sen(α) y' = x * (-sen(α)) + y * cos(α)
De donde se deduce que:
- eM11 es el coseno de α
- eM12 es el seno de α
- eM21 es menos el seno de α
- eM22 es el coseno de α
Nota:
Cuidado con los cálculos, hay que tener en cuenta que en C y C++ se usan ángulos expresados en radianes, 360º son 2π radianes (90º son π/2 radianes , y 45º son π/4 radianes). Además, las funciones trigonométricas están declaradas en el fichero de cabecera math.h, y se llaman sin y cos.
Cambio de ejes
Podemos inclinar los ejes, de forma que la transformación no sea ortogonal (es decir, que los ejes no sean perpendiculares). Bastará considerar los factores eM12 y eM21 como constantes de proporcionalidad, horizontal y vertical, respectivamente.
x' = x + y * eM21 y' = x * eM12 + y
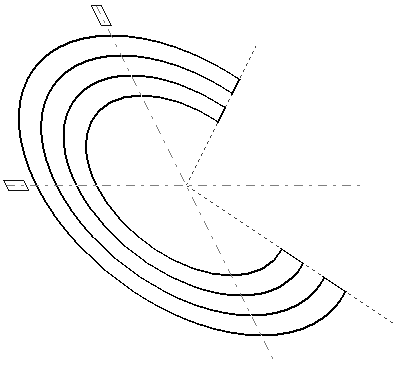
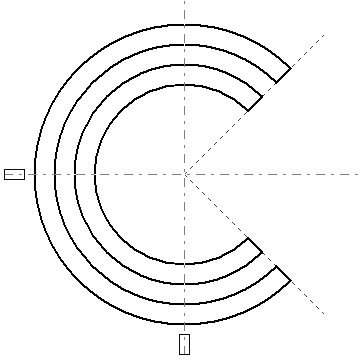
Reflexiones
Podemos cosiderar una reflexión como un caso particular de cambio de escala. Si cambiamos el signo de eM11 obtendremos una reflexión en el eje y, si cambiamos el signo de eM22 obtendremos una reflexión en el eje x.
x' = x * eM11 y' = y * eM22
Aplicar transformaciones
En el API32 hay dos modos gráficos diferentes. El compatible y el avanzado.
El compatible es el modo original de Windows 3.1 y Windows 95, y el único que existía en esos sistemas.
El modo avanzado sólo existe en el API32, para Windows NT y sistemas posteriores, como ME, 2000 y XP. Sólo en este modo es posible usar transformaciones, de modo que antes de aplicar cualquier transformación, será necesario activar el modo avanzado.
Para cambiar el modo gráfico se usa la función SetGraphicsMode, el modo gráfico se aplica a un DC, así que necesitamos un manipulador de DC. Disponemos de dos constantes para activar cada uno de los modos: GM_COMPATIBLE y GM_ADVANCED.
Una vez activado el modo avanzado, ya podemos usar transformaciones. Si no aplicamos ninguna, por defecto se usa la transformación identidad. Y si queremos activar el modo compatible, es imprescindible que la transformación actual sea la de identidad, de otro modo la función SetGraphicsMode fallará.
Para aplicar una transformación usaremos la función SetWorldTransform, que requiere un manipulador de DC y un puntero a una estructura XFORM con la transformación a aplicar.
XFORM xform = {1, 0, 0, 1, 0, 0}; // Sin transformar (matriz identidad)
...
case WM_PAINT:
hdc = BeginPaint(hwnd, &ps);
SetGraphicsMode(hdc, GM_ADVANCED);
SetWorldTransform(hdc, &xform);
// Funciones de trazado gráfico
EndPaint(hwnd, &ps);
break;
Combinar transformaciones
No tenemos que limitarnos a hacer transformaciones simples, podemos combinarlas para crear transformaciones complejas, de modo que podemos rotar, trasladar, cambiar ejes, escalar y reflejar mediante una única transformación.
Para ello disponemos de dos opciones diferentes:
Combinar dos transformaciones mediante la función CombineTransform. Esta función obtiene una transformación a partir de otras dos, el resultado de aplicar la transformación obtenida equivale a aplicar las dos transformaciones, una a continuación de la otra.
Modificar la transformación del mundo actual mediante la función ModifyWorldTransform. Mediante esta función será posible combinar la transformación actual con otra, o bien, asignar la matriz de transformación identidad (si se usa el valor MWT_IDENTITY como tercer parámetro. Este tercer parámetro admite otros dos valores: MWT_LEFTMULTIPLY y MWT_RIGHTMULTIPLY, que permite multiplicar la transformación indicada por la izquierda o por la derecha. El resultado puede ser diferente, ya que la multiplicación de matrices no posee la propiedad conmutativa.
Si necesitamos obtener la matriz de transformación actual, podemos hacer uso de la función GetWorldTransform.
Cambios de escala y plumas
Cuando se usan plumas cosméticas para trazar figuras, las únicas que hemos usado hasta ahora, el grosor del trazo se expresa en unidades lógicas, es decir, si duplicamos la escala, el grosor de las líneas se duplica. Esto es así salvo que indiquemos un grosor 0. En ese caso, las líneas siempre son de un pixel de ancho, y por lo tanto, el resultado es que parece que las líneas son más finas cuanto más grande sea la escala. Este efecto puede ser útil cuando trazamos ejes o líneas de ayuda.
Ejemplo 28
| Nombre | Fichero | Fecha | Tamaño | Contador | Descarga |
|---|---|---|---|---|---|
| Ejemplo 28 | win028.zip | 2004-06-14 | 3365 bytes | 1010 |
Ventanas y viewports
La ventana define en el espacio de coordenadas de la página, mediante dos parámetros: la extensión y el origen.
El viewport define el espacio de coordenadas del dispositivo, mediante los mismos parámetros que la ventana: la extensión, y el origen.
En el caso del viewport, al definir el espacio del dispositivo, los valores se expresan en coordendas de dispositivo, es decir, en pixels.
Los puntos en el espacio de página se expresan en coordenadas lógicas, y por lo tanto, también se usan valores lógicos en la ventana. Tanto la extensión como el origen de la ventana se expresa en valores lógicos.
No debemos confundir el espacio de página con la ventana física de la aplicación, aunque existe cierta analogía, la ventana de la que hablamos ahora es un concepto de espacio gráfico, no siempre ligado a la ventana que se muestra en el monitor, es más bien, una ventana que nos permite ver parte del espacio gráfico total.
Extensiones
En el caso de la ventana la extensión se ajusta por la función SetWindowExtEx. También existe una función para obtener ese parámetro: GetWindowExtEx.
Para le viewport también existe una pareja de funciones para asignar y leer la extensión: SetViewportExtEx y GetViewportExtEx.
Orígenes
Tanto en el caso de la ventana como en el del viewport, podemos definir un origen de coordenadas, en el caso de la ventana se usa la función SetWindowOrgEx y en el caso del viewport, la función SetViewportOrgEx. Por supuesto, existen las funciones simétricas, para leer esas coordenadas: GetWindowOrgEx y GetViewportOrgEx.
Mapeos
Podríamos titular este apartado como transformaciones del espacio de página al de dispositivo.
Para realizar estas transformaciones se usan los valores de extensión y origen de la ventana y del viewport. Los puntos situados en la ventana se proyectan (o se mapean) al espacio del viewport. Las fórmulas para hacer esas proyecciones son simples:
Dx = ((Lx - WOx) * VEx / WEx) + VOx Dy = ((Ly - WOy) * VEy / WEy) + VOy
Donde:
- (Dx,Dy) son las coordenadas del punto en unidades de dispositivo.
- (Lx,Ly) las coordenadas del puntir en unidades lógicas (unidades del espacio de página).
- (WOx,WOy) las coordenadas del origen de la ventana.
- (VOx,VOy) las coordenadas del origen del viewport.
- (WEx,WEy) es la extensión de la ventana.
- (VEx,VEy) la extensión del viewport.
Básicamente, estas fórmulas definen un cambio de escala, y una traslación.
Existen dos funciones para realizar estos cálculos, así como sus inversos. Podemos, de este modo, pasar las coordenadas de un punto de un espacio al otro. Para pasar un punto en coordendadas lógicas (de página) a coordenadas de dispositivo, se usa la función LPtoDP. Para pasar de coordenadas de dispositivo a coordenadas lógicas, se usar la función DPtoLP.
Modos de mapeo predefinidos
En Windows existen ocho posibles modos de mapeo, cada uno con sus características propias:
- Isotrópico: el mapeo entre el espacio de página y el del dispositivo se define por la aplicación, cambiando las extensiones y orígenes de la ventana y del viewport. Las medidas en ambos ejes son iguales, pero la orientación se puede definir por la aplicación.
- No isotrópico: igual que el anterior, pero las medidas en el eje x no tienen por qué ser iguales que en el eje y.
- Inglés alto: cada unidad del espacio de página se mapea a 0.001 pulgadas en el espacio de dispositivo. Las x crecen hacia la derecha, las y hacia arriba.
- Inglés bajo: cada unidad del espacio de página se mapea a 0.01 pulgadas en el espacio de dispositivo. Las x crecen hacia la derecha, las y hacia arriba.
- Métrico alto: cada unidad del espacio de página se mapea a 0.01 milímetros en el espacio de dispositivo. Las x crecen hacia la derecha, las y hacia arriba.
- Métrico bajo: cada unidad del espacio de página se mapea a 0.1 milímetros en el espacio de dispositivo. Las x crecen hacia la derecha, las y hacia arriba.
- Texto: cada unidad del espacio de página se mapea a un pixel, es decir, no se hace ningún cambio de escala.
- Twips: cada unidad del espacio de página se mapea a 1/20 de punto de impresora (un twip), que equivale a 1/1440 de pulgada. Las x crecen hacia la derecha, las y hacia arriba.
Para activar un modo de mapeo se usa la función SetMapMode. Esta función precisa dos parámetros: un manipulador de DC, y el identificador del modo de mapeo (MM_ISOTROPIC, MM_ANISOTROPIC, MM_HIENGLISH, MM_LOENGLISH, MM_HIMETRIC, MM_LOMETRIC, MM_TEXT y MM_TWIPS, respectivamente). Para averiguar el modo actual GetMapMode.
En el caso de los seis últimos modos (todos menos el isotrópico y el no isotrópico), la extensión del viewport no puede alterarse, ya que se ajusta automáticamente, en función de la extensión de la ventana.
Cuando se usan los modos isotrópico o no isotrópico, es necesario ajustar la extensión y origen del viewport, ya que en estos modos, el cambio de escala se define por la aplicación. En el caso del modo isotrópico es importante ajustar la extensión de la ventana antes de hacerlo con el viewport.
Modo por defecto
El modo por defecto es el de texto, que además es el único que es dependiente del dispositivo.
Este modo es útil si la salida sólo se va a visualizar en pantalla, pero no resultará muy conveniente si tenemos que asegurar que el tamaño de nuestros gráficos es real (por ejemplo si dibujamos un cuadrado de 10 centímetros de lado), y mucho menos si tenemos que realizar salidas a impresora, si trazamos un cuadrado de 100 pixels en pantalla, el tamaño en impresora dependerá mucho de los puntos por pulgada de resolución que tenga la impresora.
En cada caso será interesante escoger un modo independiente de dispositivo, ya sea en pulgadas, milímetros, o puntos de impresora.
Transformaciones definidas por el usuario
Hay dos modos de mapeo que implican que la transformación se difine por el usuario: el isotrópico y el no isotrópico. Son modos muy similares, pero el isotrópico asegura que las unidades lógicas son del mismo tamaño en el eje x y el en eje y. El modo no isotrópico permite usar unidades diferentes en cada eje.
Por ejemplo, para obtener una resolución de 1/3 milímetro, podemos usar el modo isotrópico de esta manera:
SetMapMode(hDC, MM_ISOTROPIC);
SetWindowExtEx(hDC, 3*GetDeviceCaps(hDC, HORZSIZE),
3*GetDeviceCaps(hDC, VERTSIZE), NULL);
SetViewportExtEx(hDC, GetDeviceCaps(hDC, HORZRES),
GetDeviceCaps(hDC, VERTRES), NULL);
Invocamos la función GetDeviceCaps para obtener las dimensiones del dispositivo en milímetros (HORZSIZE,VERTSIZE), y el pixels (HORZRES,VERTRES). Hacemos que la extensión x e y de la ventana sea el triple del tamaño del dispositivo en milímetros, y que la extensión del viewport sea el tamaño del dispositivo en pixels. Esto hace que cada unidad de página (unidad lógica) se convierta en 1/3 milímetro.
Modos gráficos y sentido de los arcos
Hay que tener en cuenta que el sentido en que se trazan los arcos es importante, y que el resultado de la salida gráfica dependerá del modo gráfico y del modo de mapeo seleccionados, y en el caso de los modos isotrópico y no isotrópico, de los signos de los valores de las extensiones de ventana y viewport.
En el modo gráfico avanzado, los arcos siempre se trazan en el sentido de las agujas del reloj en el espacio lógico. Esto independiza la salida del modo de mapeo elegido. En el caso del modo gráfico compatible se usa el sentido de trazado actual de los arcos para trazarlos en el espacio del dispositivo, es decir, una vez aplicado el mapeo. De modo que si cambiamos el modo de mapeo, el aspecto de los arcos puede cambiar.
Recordemos que podemos cambiar el sentido de trazado de los arcos en el espacio de dispositivo, usando la función SetArcDirection.
Nota:
Siempre que podamos, usaremos el modo gráfico avanzado, ya que no sólo nos permite usar transformaciones, sino que además simplifica el trazado de arcos, al no tener que preocuparse del modo de mapeo que se use en cada caso.
Otras funciones
Hay algunas funciones más relacionadas con espacios de coordenadas:
| ClientToScreen | Convierte coordenadas de cliente a coordenadas de pantalla. |
| ScreenToClient | Convierte coordenadas de pantalla a coordenadas de cliente. |
| GetCurrentPositionEx | Recupera la posición actual del cursor gráfico en coordenadas lógicas. |
| OffsetWindowOrgEx | Desplaza el origen de la ventana en las cantidades especificadas. |
| OffsetViewportOrgEx | Desplaza el origen del viewport en las cantidades especificadas. |
| ScaleWindowExtEx | Modifica la extensión de la ventana en el factor especificado. |
| ScaleViewportExtEx | Modifica la extensión del viewport en el factor especificado. |
Ejemplo 29
| Nombre | Fichero | Fecha | Tamaño | Contador | Descarga |
|---|---|---|---|---|---|
| Ejemplo 29 | win029.zip | 2004-06-14 | 3432 bytes | 1061 |