3 Diseño de bases de datos:
El modelo lógico, modelo relacional

Modelo relacional

Entre los modelos lógicos, el modelo relacional está considerado como el más simple. No vamos a entrar en ese tema, puesto que es el único que vamos a ver, no tiene sentido establecer comparaciones.

Diremos que es el que más nos conviene. Por una parte, el paso del modelo E-R al relacional es muy simple, y por otra, MySQL, como implementación de SQL, está orientado principalmente a bases de datos relacionales.

El modelo se compone de tres partes:

1. Estructura de datos: básicamente se compone de relaciones.
2. Manipulación de datos: un conjunto de operadores para recuperar, derivar o modificar los datos almacenados.
3. Integridad de datos: una colección de reglas que definen la consistencia de la base de datos.

Definiciones

Igual que hicimos con el modelo E-R, empezaremos con algunas definiciones. Algunos de los conceptos son comunes entre los dos modelos, como atributo o dominio. Pero de todos modos, los definiremos de nuevo.

Relación

Es el concepto básico del modelo relacional. Ya adelantamos en el capítulo anterior que los conceptos de relación entre el modelo E-R y el relacional son diferentes. Por lo tanto, usamos el término interrelación para referirnos a la conexión entre entidades. En el modelo relacional este término se refiere a una tabla, y es el paralelo al concepto conjunto de entidades del modelo E-R.

Relación: es un conjunto de datos referentes a un conjunto de entidades y organizados en forma tabular, que se compone de filas y columnas, (tuplas y atributos), en la que cada intersección de fila y columna contiene un valor.

Tupla

A menudo se le llama también registro o fila, físicamente es cada una de las líneas de la relación. Equivale al concepto de entidad del modelo E-R, y define un objeto real, ya sea abstracto, concretos o imaginario.

Tupla: cada una de las filas de una relación. Contiene la información relativa a una única entidad.

De esta definición se deduce que no pueden existir dos tuplas iguales en la misma relación.

Atributo

También denominado campo o columna, corresponde con las divisiones verticales de la relación. Corresponde al concepto de atributo del modelo E-R y contiene cada una de las características que definen una entidad u objeto.

Atributo: cada una de las características que posee una entidad, y que agrupadas permiten distingirla de otras entidades del mismo conjunto.

Al igual que en el modelo E-R, cada atributo tiene asignado un nombre y un dominio. El conjunto de todos los atributos es lo que define a una entidad completa, y es lo que compone una tupla.

Nulo (NULL)

Hay ciertos atributos, para determinadas entidades, que carecen de valor. El modelo relacional distingue entre valores vacíos y valores nulos. Un valor vacío se considera un valor tanto como cualquiera no vacío, sin embargo, un nulo NULL indica la ausencia de valor.

Nulo: (NULL) valor asignado a un atributo que indica que no contiene ninguno de los valores del dominio de dicho atributo.

El nulo es muy importante en el modelo relacional, ya que nos permite trabajar con datos desconocidos o ausentes.

Por ejemplo, si tenemos una relación de vehículos en la que podemos guardar tanto motocicletas como automóviles, un atributo que indique a qué lado está el volante (para distinguir vehículos con el volante a la izquierda de los que lo tienen a la derecha), carece de sentido en motocicletas. En ese caso, ese atributo para entidades de tipo motocicleta será NULL.

Esto es muy interesante, ya que el dominio de este atributo es (derecha,izquierda), de modo que si queremos asignar un valor del dominio no hay otra opción. El valor nulo nos dice que ese atributo no tiene ninguno de los valores posibles del dominio. Así que, en cierto modo amplia la información.

Otro ejemplo, en una relación de personas tenemos un atributo para la fecha de nacimiento. Todas las personas de la relación han nacido, pero en un determinado momento puede ser necesario insertar una para la que desconocemos ese dato. Cualquier valor del dominio será, en principio, incorrecto. Pero tampoco será posible distinguirlo de los valores correctos, ya que será una fecha. Podemos usar el valor NULL para indicar que la fecha de nacimiento es desconocida.

Dominio

Dominio: Rango o conjunto de posibles valores de un atributo.

El concepto de dominio es el mismo en el modelo E-R y en el modelo relacional. Pero en este modelo tiene mayor importancia, ya que será un dato importante a la hora de dimensionar la relación.

De nuevo estamos ante un concepto muy flexible. Por ejemplo, si definimos un atributo del tipo entero, el dominio más amplio sería, lógicamente, el de los números enteros. Pero este dominio es infinito, y sabemos que los ordenadores no pueden manejar infinitos números enteros. Al definir un atributo de una relación dispondremos de distintas opciones para guardar datos enteros. Si en nuestro caso usamos la variante de "entero pequeño", el dominio estará entre -128 y 127. Pero además, el atributo corresponderá a una característica concreta de una entidad; si se tratase, por ejemplo, de una calificación sobre 100, el dominio estaría restringido a los valores entre 0 y 100.

Modelo relacional

Ahora ya disponemos de los conceptos básicos para definir en qué consiste el modelo relacional. Es un modelo basado en relaciones, en la que cada una de ellas cumple determinadas condiciones mínimas de diseño:

• No deben existir dos tuplas iguales.
• Cada atributo sólo puede tomar un único valor del dominio, es decir, no pueden contener listas de valores.
• El orden de las tuplas dentro de la relación y el de los atributos, dentro de cada tupla, no es importante.

Cardinalidad

Cardinalidad: número de tuplas que contiene una relación.

La cadinalidad puede cambiar, y de hecho lo hace frecuentemente, a lo largo del tiempo: siempre se pueden añadir y eliminar tuplas.

Grado

Grado: número de atributos de cada tupla.

El grado de una relación es un valor constante. Esto no quiere decir que no se puedan agregar o eliminar atributos de una relación; lo que significa es que si se hace, la relación cambia. Cambiar el grado, generalmente, implicará modificaciones en las aplicaciones que hagan uso de la base de datos, ya que cambiarán conceptos como claves e interrelaciones, de hecho, puede cambiar toda la estructura de la base de datos.

Esquema

Esquema: es la parte constante de una relación, es decir, su estructura.

Esto es, el esquema es una lista de los atributos que definen una relación y sus dominios.

Instancia

Instancia: es el conjunto de las tuplas que contiene una relación en un momento determinado.

Es como una fotografía de la relación, que sólo es válida durante un periodo de tiempo concreto.

Clave

Clave: es un conjunto de atributos que identifica de forma unívoca a una tupla. Puede estar compuesto por un único atributo o una combinación de varios.

Dentro del modelo relacional no existe el concepto de clave múltiple. Cada clave sólo puede hacer referencia a una tupla de una tabla. Por lo tanto, todas las claves de una relación son únicas.

Podemos clasificar las claves en distintos tipos:

• Candidata: cada una de las posibles claves de una relación, en toda relación existirá al menos una clave candidata. Esto implica que ninguna relación puede contener tuplas repetidas.
• Primaria: (o principal) es la clave candidata elegida por por el usuario para identificar las tuplas. No existe la necesidad, desde el punto de vista de la teoría de bases de datos relacionales, de elegir una clave primaria. Además, las claves primarias no pueden tomar valores nulos.
  Es preferible, por motivos de optimización de MySQL, que estos valores sean enteros, aunque no es obligatorio. MySQL sólo admite una clave primaria por tabla, lo cual es lógico, ya que la definición implica que sólo puede existir una.
• Alternativa: cada una de las claves candidatas que no son clave primaria, si es que existen.
• Foránea: (o externa) es el atributo (o conjunto de atributos) dentro de una relación que contienen claves primarias de otra relación. No hay nada que impida que ambas relaciones sean la misma.

Interrelación

Decimos que dos relaciones están interrelacionadas cuando una posee una clave foránea de la otra. Cada una de las claves foráneas de una relación establece una interrelación con la relación donde esa clave es la principal.

Según esto, existen dos tipos de interrelación:

• La interrelación entre entidades fuertes y débiles.
• La interreación pura, entre entidades fuertes.

Extrictamente hablando, sólo la segunda es una interrelación, pero como veremos más tarde, en el modelo relacional ambas tienen la forma de relaciones, al igual que las entidades compuestas, que son interrelaciones con atributos añadidos.

Al igual que en el modelo E-R, existen varios tipos de interrelación:

• Uno a uno: a cada tupla de una relación le corresponde una y sólo una tupla de otra.
• Uno a varios: a cada tupla una relación le corresponden varias en otra.
• Varios a varios: cuando varias tuplas de una relación se pueden corresponder con varias tuplas en otra.

Paso del modelo E-R al modelo relacional

Existen varias reglas para convertir cada uno de los elementos de los diagramas E-R en tablas:

1. Para cada conjunto de entidades fuertes se crea una relación con una columna para cada atributo.
2. Para cada conjunto de entidades débiles se crea una relación que contiene una columna para los atributos que forman la clave primaria de la entidad fuerte a la que se encuentra subordinada y una columna para cada atributo de la entidad.
3. Para cada interrelación se crea una relación que contiene una columna para cada atributo correspondiente a las claves principales de las entidades interrelacionadas.
4. Lo mismo para entidades compuestas, añadiendo las columnas necesarias para los atributos añadidos a la interrelación.

Las relaciones se representan mediante sus esquemas, la sintaxis es simple:

<nombre_relación>(<nombre_atributo_i>,...)

La clave principal se suele indicar mediante un subrayado.

Veamos un ejemplo, partamos del siguiente diagrama E-R:

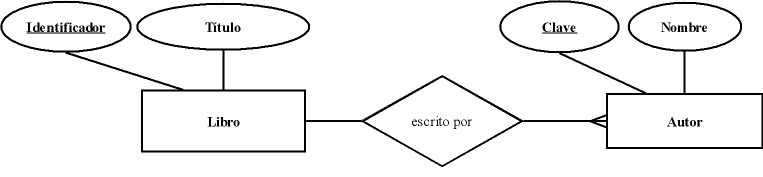
Siguiendo las normas indicadas obtendremos las siguientes relaciones:

Libro(Identificador, Título)
Autor(Clave, Nombre)
Escrito_por(Identificador, Clave)

Manipulación de datos, álgebra relacional

El modelo relacional también define el modo en que se pueden manipular las relaciones. Hay que tener en cuenta que este modelo tiene una base matemática muy fuerte. Esto no debe asustarnos, en principio, ya que es lo que le proporciona su potencia y seguridad. Es cierto que también complica su estudio, pero afortunadamente, no tendremos que comprender a fondo la teoría para poder manejar el modelo.

En el modelo relacionar define ciertos operadores. Estos operadores relacionales trabajan con tablas, del mismo modo que los operadores matemáticos trabajan con números. Esto implica que el resultado de las operaciones con relaciones son relaciones, lo cual significa que, como veremos, no necesitaremos implementar bucles.

El álgebra relacional define el modo en que se aplican los operadores relacionales sobre las relaciones y los resultados que se obtienen. Del mismo modo que al aplicar operadores enteros sobre números enteros sólo da como salida números enteros, en álgebra relacional los resultados de aplicar operadores son relaciones.

Disponemos de varios operadores, que vamos a ver a continuación.

Selección

Se trata de un operador unitario, es decir, se aplica a una relación y como resultado se obtiene otra relación.

Consiste en seleccionar ciertas tuplas de una relación. Generalmente la selección se limita a las tuplas que cumplan determinadas condiciones.

<relación>[<atributo>='<valor>']

Por ejemplo, tengamos la siguiente relación:

tabla(id, nombre, apellido, fecha, estado)

tabla
id   nombre   apellido    fecha       estado
123  Fulano   Prierez     4/12/1987   soltero
454  Mengano  Sianchiez   15/1/1990   soltero
102  Tulana   Liopez      24/6/1985   casado
554  Filgana  Gaomez      15/5/1998   soltero
005  Tutulano Gionzialez  2/6/1970    viudo

Algunos ejemplos de selección serían:

tabla[id<'200']
id   nombre   apellido    fecha       estado
123  Fulano   Prierez     4/12/1987   soltero
102  Tulana   Liopez      24/6/1985   casado
005  Tutulano Gionzialez  2/6/1970    viudo

tabla[estado='soltero']
123  Fulano   Prierez     4/12/1987   soltero
454  Mengano  Sianchiez   15/1/1990   soltero
554  Filgana  Gaomez      15/5/1998   soltero

Proyección

También es un operador unitario.

Consiste en seleccionar ciertos atributos de una relación.

Esto puede provocar un conflicto. Como la relación resultante puede no incluir ciertos atributos que forman parte de la clave principal, existe la posibilidad de que haya tuplas duplicadas. En ese caso, tales tuplas se eliminan de la relación de salida.

<relación>[<lista de atributos>]

Por ejemplo, tengamos la siguiente relación:

tabla(id, nombre, apellido, fecha, estado)

tabla
id   nombre   apellido    fecha       estado
123  Fulano   Prierez     4/12/1987   soltero
454  Mengano  Sianchiez   15/1/1990   soltero
102  Tulana   Liopez      24/6/1985   casado
554  Fulano   Gaomez      15/5/1998   soltero
005  Tutulano Gionzialez  2/6/1970    viudo

Algunos ejemplos de proyección serían:

tabla[id,apellido]
id   apellido
123  Prierez
454  Sianchiez
102  Liopez
554  Gaomez
005  Gionzialez

tabla[nombre, estado]
nombre   estado
Fulano   soltero
Mengano  soltero
Tulana   casado
Tutulano viudo

En esta última proyección se ha eliminado una tupla, ya que aparece repetida. Las tuplas 1ª y 4ª son idénticas, las dos personas de nombre 'Fulano' son solteras.

Producto cartesiano

Este es un operador binario, se aplica a dos relaciones y el resultado es otra relación.

El resultado es una relación que contendrá todas las combinaciones de las tuplas de los dos operandos.

Esto es: si partimos de dos relaciones, R y S, cuyos grados son n y m, y cuyas cardinalidades a y b, la relación producto tendrá todos los atributos presentes en ambas relaciones, por lo tanto, el grado será n+m. Además la cardinalidad será el producto de a y b.

Para ver un ejemplo usaremos dos tablas inventadas al efecto:

tabla1(id, nombre, apellido)
tabla2(id, número)

tabla1
id  nombre     apellido
15  Fulginio   Liepez
26  Cascanio   Suanchiez

tabla2
id   número
15   12345678
26   21222112
15   66525425

El resultado del producto cartesiano de tabla1 y tabla2: tabla1 x tabla2 es:

tabla1 x tabla2
id  nombre     apellido   id   número
15  Fulginio   Liepez     15   12345678
26  Cascanio   Suanchiez  15   12345678
15  Fulginio   Liepez     26   21222112
26  Cascanio   Suanchiez  26   21222112
15  Fulginio   Liepez     15   66525425
26  Cascanio   Suanchiez  15   66525425

Podemos ver que el grado resultante es 3+2=5, y la cardinalidad 2*3 = 6.

Composición (Join)

Una composición (Join en inglés) es una restricción del producto cartesiano, en la relación de salida sólo se incluyen las tuplas que cumplan una determinada condición.

La condición que se usa más frecuentemente es la igualdad entre dos atributos, uno de cada tabla.

<relación1>[<condición>]<relación2>

Veamos un ejemplo. Partimos de dos relaciones:

tabla1(id, nombre, apellido)
tabla2(id, número)

tabla1
id  nombre     apellido
15  Fulginio   Liepez
26  Cascanio   Suanchiez

tabla2
id   número
15   12345678
26   21222112
15   66525425

La composición de estas dos tablas, para una condición en que 'id' sea igual en ambas sería:

tabla1[tabla1.id = tabla2.id]tabla2
id  nombre     apellido   t2.id   número
15  Fulginio   Liepez     15      12345678
26  Cascanio   Suanchiez  26      21222112
15  Fulginio   Liepez     15      66525425

Composición natural

Cuando la condición es la igualdad entre atributos de cada tabla, la relación de salida tendrá parejas de columnas con valores iguales, por lo tanto, se podrá eliminar siempre una de esas columnas. Cuando se eliminan, el tipo de composición se denomina composición natural.

El grado, por lo tanto, en una composición natural es n+m-i, siendo i el número de atributos comparados entre ambas relaciones. La cardinalidad de la relación de salida depende de la condición.

Si sólo se compara un atributo, el grado será n+m-1, si se comparan dos atributos, el grado será n+m-2, y generalizando, si se comparan i atributos, el grado será n+m-i.

En el ejemplo anterior, si hacemos una composición natural, la columna t2.a1 no aparecería, ya que está repetida:

La composición natural de estas dos tablas, para una condición en que 'id' sea igual en ambas sería:

tabla1[tabla1.id = tabla2.id]tabla2
id  nombre     apellido   número
15  Fulginio   Liepez     12345678
26  Cascanio   Suanchiez  21222112
15  Fulginio   Liepez     66525425

Podemos hacer una composición natural en la que intervengan dos atributos.

tabla1(x, y, nombre)
tabla2(x, y, número)

tabla1
x  y   nombre
A  4   Fulginio
A  6   Cascanio
B  3   Melania
C  4   Juaninia
C  7   Antononio
D  2   Ferninio
D  5   Ananinia

tabla2
x  y  número
A  3  120
A  6  145
B  2  250
B  5  450
C  4  140
D  2  130
D  5  302

Si la condición es que tanto 'x' como 'y' sean iguales en ambas tablas, tendríamos:

tabla1[tabla1.x = tabla2.x Y tabla1.y = tabla2.y]tabla2
x  y   nombre   número
A  6   Cascanio 145
C  4   Juaninia 140
D  2   Ferninio 130
D  5   Ananinia 302

Unión

También se trata de un operador binario.

Una unión es una suma. Ya sabemos que para poder sumar, los operandos deben ser del mismo tipo (no podemos sumar peras y limones), es decir, las relaciones a unir deben tener el mismo número de atributos, y además deben ser de dominios compatibles. El grado de la relación resultante es el mismo que el de las relaciones a unir, y la cardinalidad es la suma de las cardinalidades de las relaciones.

<relación1> U <relación2>

Por ejemplo, tengamos estas tablas:

tabla1(id, nombre, apellido)
tabla2(id, nombre, apellido)

tabla1
id    nombre       apellido
15    Fernandio    Garcidia
34    Augustido    Lipoez
12    Julianino    Sianchiez
43    Carlanios    Pierez

tabla2
id    nombre       apellido
44    Rosinia      Ortiegaz
63    Anania       Pulpez
55    Inesiana     Diominguez

La unión de ambas tablas es posible, ya que tienen el mismo número y tipo de atributos:

tabla1 U tabla2
id    nombre       apellido
15    Fernandio    Garcidia
34    Augustido    Lipoez
12    Julianino    Sianchiez
43    Carlanios    Pierez
44    Rosinia      Ortiegaz
63    Anania       Pulpez
55    Inesiana     Diominguez

Intersección

El operador de intersección también es binario.

Para que dos relaciones se puedan interseccionar deben cumplir las mismas condiciones que para que se puedan unir. El resultado es una relación que contendrá sólo las tuplas presentes en ambas relaciones.

<relación1> intersección <relación2>

Por ejemplo, tengamos estas tablas:

tabla1(id, prenda, color)
tabla2(id, prenda, color)

tabla1
id    prenda    color
10    Jersey    Blanco
20    Jersey    Azul
30    Pantalón  Verde
40    Falda     Roja
50    Falda     Naranja

tabla2
id    prenda    color
15    Jersey    Violeta
20    Jersey    Azul
34    Pantalón  Amarillo
40    Falda     Roja
52    Falda     Verde

Es posible obtener la intersección de ambas relaciones, ya que tienen el mismo número y tipo de atributos:

tabla1 intersección tabla2
id    prenda    color
20    Jersey    Azul
40    Falda     Roja

Diferencia

Otro operador binario más.

Los operandos también deben cumplir las mismas condiciones que para la unión o la intersección. El resultado es una relación que contiene las tuplas de la primera relación que no estén presentes en la segunda.

<relación1> - <relación2>

Por ejemplo, tengamos estas tablas:

tabla1(id, prenda, color)
tabla2(id, prenda, color)

tabla1
id    prenda    color
10    Jersey    Blanco
20    Jersey    Azul
30    Pantalón  Verde
40    Falda     Roja
50    Falda     Naranja

tabla2
id    prenda    color
15    Jersey    Violeta
20    Jersey    Azul
34    Pantalón  Amarillo
40    Falda     Roja
52    Falda     Verde

Es posible obtener la diferencia de ambas relaciones, ya que tienen el mismo número y tipo de atributos:

tabla1 - tabla2
id    prenda    color
10    Jersey    Blanco
30    Pantalón  Verde
50    Falda     Naranja

División

La operación inversa al producto cartesiano.

Este tipo de operación es poco frecuente, las relaciones que intervienen como operandos deben cumplir determinadas condiciones, de divisibilidad, que hace difícil encontrar situaciones en que se aplique.

Integridad de datos

Es muy importante impedir situaciones que hagan que los datos no sean accesibles, o que existan datos almacenados que no se refieran a objetos o entidades existentes, etc. El modelo relacional también provee mecanismos para mantener la integridad. Podemos dividir estos mecanismos en dos categorías:

• Restricciones estáticas, que se refieren a los estados válidos de datos almacenados.
• Restricciones dinámicas, que definen las acciones a realizar para evitar ciertos efectos secundarios no deseados cuando se realizan operaciones de modificación o borrado de datos.

Restricciones sobre claves primarias

En cuanto a las restricciones estáticas, las más importantes son las que afectan a las claves primarias.

Ninguna de las partes que componen una clave primaria puede ser NULL.

Que parte de una clave primaria sea NULL indicaría que, o bien esa parte no es algo absolutamente necesario para definir la entidad, con lo cual no debería formar parte de la clave primaria, o bien no sabemos a qué objeto concreto nos estamos refiriendo, lo que implica que estamos tratando con un grupo de entidades. Esto va en contra de la norma que dice que cada tupla contiene datos sólo de una entidad.

Las modificaciones de claves primarias deben estar muy bien controladas.

Dado que una clave primaria identifica de forma unívoca a una tupla en una relación, parece poco lógico que exista necesidad de modificarla, ya que eso implicaría que no estamos definiendo la misma entidad.

Además, hay que tener en cuenta que las claves primarias se usan frecuentemente para establecer interrelaciones, lo cual implica que sus valores se usan en otras relaciones. Si se modifica un valor de una clave primaria hay que ser muy cuidadoso con el efecto que esto puede tener en todas las relaciones en las que se guarden esos valores.

Existen varias maneras de limitar la modificación de claves primarias. Codd apuntó tres posibilidades:

• Que sólo un número limitado de usuarios puedan modificar los valores de claves primarias. Estos usuarios deben ser conscientes de las repercusiones de tales cambios, y deben actuar de modo que se mantenga la integridad.
• La prohibición absoluta de modificar los valores de claves primarias. Modificarlas sigue siendo posible, pero mediante un mecanismo indirecto. Primero hay que eliminar las tuplas cuyas claves se quieren modificar y a continuación darlas de alta con el nuevo valor de clave primaria.
• La creación de un comando distinto para modificar atributos que son claves primarias o partes de ellas, del que se usa para modificar el resto de los atributos.

Cada SGBD puede implementar alguno o varios de estos métodos.

Integridad referencial

La integridad referencial se refiere a las claves foráneas. Recordemos que una clave foránea es un atributo de una relación, cuyos valores se corresponden con los de una clave primaria en otra o en la misma relación. Este mecanismo se usa para establecer interrelaciones.

La integridad referencial consiste en que si un atributo o conjunto de atributos se define como una clave foránea, sus valores deben existir en la tabla en que ese atribito es clave principal.

Las situaciones donde puede violarse la integridad referencial es en el borrado de tuplas o en la modificación de claves principales. Si se elimina una tupla cuya clave primaria se usa como clave foránea en otra relación, las tuplas con esos valores de clave foránea contendrán valores sin referenciar.

Existen varias formas de asegurarse de que se conserva la integridad referencial:

• Restringir operaciones: borrar o modificar tuplas cuya clave primaria es clave foránea en otras tuplas, sólo estará permitido si no existe ninguna tupla con ese valor de clave en ninguna otra relación.
  Es decir, si el valor de una clave primaria en una tupla es "clave1", sólo podremos eliminar esa tupla si el valor "clave1" no se usa en ninguna otra tupla, de la misma relación o de otra, como valor de clave foránea.
• Transmisión en cascada: borrar o modificar tuplas cuya clave primaria es clave foránea en otras implica borrar o modificar las tuplas con los mismos valores de clave foránea.
  Si en el caso anterior, modificamos el valor de clave primaria "clave1" por "clave2", todas las apariciones del valor "clave1" en donde sea clave foránea deben ser sustituidos por "clave2".
• Poner a nulo: cuando se elimine una tupla cuyo valor de clave primaria aparece en otras relaciones como clave foránea, se asigna el valor NULL a dichas claves foráneas.
  De nuevo, siguiendo el ejemplo anterior, si eliminamos la tupla con el valor de clave primaria "clave1", en todas las tuplas donde aparezca ese valor como clave foránea se sustituirá por NULL.

Veremos con mucho más detalle como se implementan estos mecanismos en MySQL al estudiar el lenguaje SQL.

Propagación de claves

Se trata de un concepto que se aplica a interrelaciones N:1 ó 1:1, que nos ahorra la creación de una relación. Supongamos las siguientes relaciones, resultado del paso del ejemplo 2 del modelo E-R al modelo relacional:

Libro(ClaveLibro, Título, Idioma, Formato, Categoría)
Editado_por(ClaveLibro, ClaveEditorial)
Editorial(ClaveEditorial, Nombre, Dirección, Teléfono)

Cada libro sólo puede estar editado por una editorial, la interrelación es N:1. En este caso podemos prescindir de la relación Editado_por añadiendo un atributo a la relación Libro, que sea la clave primaria de la editorial:

Libro(ClaveLibro, Título, Idioma, Formato, Categoría, ClaveEditorial)
Editorial(ClaveEditorial, Nombre, Dirección, Teléfono)

A esto se le denomina propagación de la clave de la entidad Editorial a la entidad Libro.

Por supuesto, este mecanismo no es válido para interrelaciones de N:M, como por ejemplo, la que existe entre Libro y Autor.

Ejemplo 1

Para ilustrar el paso del modelo E-R al modelo relacional, usaremos los mismos ejemplos que en el capítulo anterior, y convertiremos los diagramas E-R a tablas.

Empecemos con el primer ejemplo:

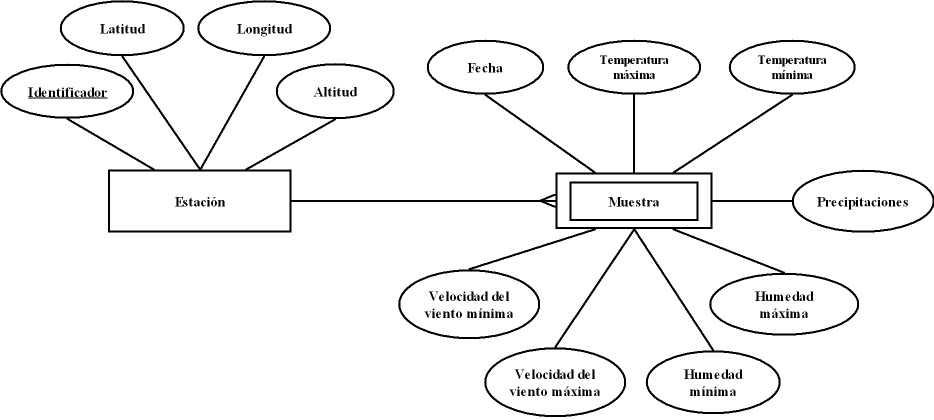
Sólo necesitamos dos tablas para hacer la conversión:

Estación(Identificador, Latitud, Longitud, Altitud)
Muestra(IdentificadorEstacion, Fecha, Temperatura mínima, Temperatura máxima,
  Precipitaciones, Humedad mínima, Humedad máxima, Velocidad del viento mínima,
  Velocidad del viento máxima)

Este ejemplo es muy simple, la conversión es directa. Se puede observar cómo hemos introducido un atributo en la relación Muestra que es el identificador de estación. Este atributo se comporta como una clave foránea.

Ejemplo 2

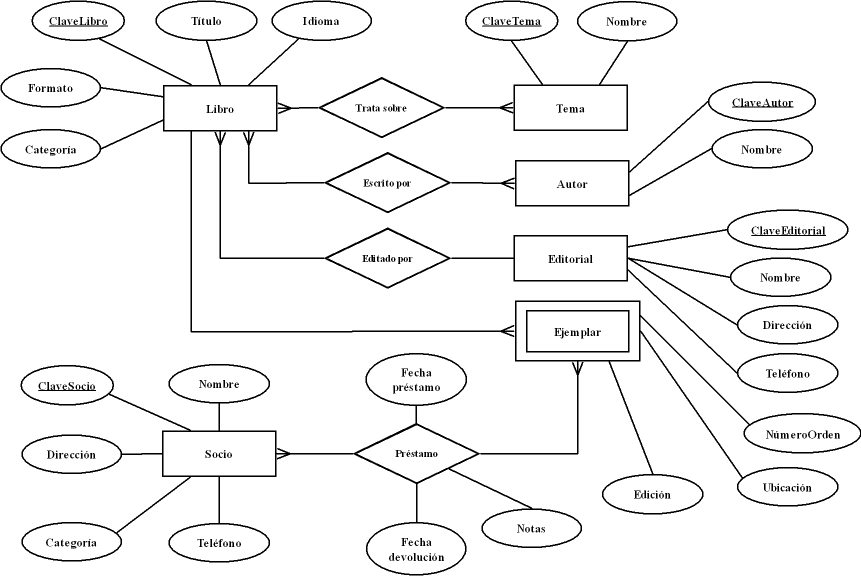
Este ejemplo es más complicado, de modo que iremos por fases. Para empezar, convertiremos los conjuntos de entidades en relaciones:

Libro(ClaveLibro, Título, Idioma, Formato)
Tema(ClaveTema, Nombre)
Autor(ClaveAutor, Nombre)
Editorial(ClaveEditorial, Nombre, Dirección, Teléfono)
Ejemplar(ClaveEjemplar, ClaveLibro, NúmeroOrden, Edición, Ubicación, Categoría)
Socio(ClaveSocio, Nombre, Dirección, Teléfono, Categoría)

Recordemos que Préstamo es una entidad compuesta:

Préstamo(ClaveSocio, ClaveEjemplar, Fecha_préstamo, Fecha_devolución, Notas)

La entidad Ejemplar es subordinada de Libro, es decir, que su clave principal se podría construir a partir de la clave principal de Libro y el atributo NúmeroOrden. Sin embargo crearemos una clave específica para ello.

Ahora veamos la conversión de las interrelaciones:

Trata_sobre(ClaveLibro, ClaveTema)
Escrito_por(ClaveLibro, ClaveAutor)
Editado_por(ClaveLibro, ClaveEditorial)

Ya vimos que podemos aplicar la propagación de claves entre conjuntos de entidades que mantengan una interrelación N:1 ó 1:1. En este caso, la interrelación entre Libro y Editorial cumple esa condición, de modo que podemos eliminar una interrelación y propagar la clave de Editorial a la entidad Libro.

El esquema final queda así:

Libro(ClaveLibro, Título, Idioma, Formato, ClaveEditorial)
Tema(ClaveTema, Nombre)
Autor(ClaveAutor, Nombre)
Editorial(ClaveEditorial, Nombre, Dirección, Teléfono)
Ejemplar(ClaveEjemplar, ClaveLibro, NúmeroOrden, Edición, Ubicación, Categoría)
Socio(ClaveSocio, Nombre, Dirección, Teléfono, Categoría)
Préstamo(ClaveSocio, ClaveEjemplar, Fecha_préstamo, Fecha_devolución, Notas)
Trata_sobre(ClaveLibro, ClaveTema)
Escrito_por(ClaveLibro, ClaveAutor)