Capítulo 10 Montículos binarios

Siguiendo con las estructuras en forma de árbol, nos encontramos con la siguiente: los montículos.

Existen varios tipos de montículos (heap, en inglés). Empezaremos por el más sencillo, los montículos binarios.

10.1 Qué son

Básicamente, se trata de árboles binarios balanceados, como los árboles AVL, la diferencia de altura de cada rama no es mayor de uno. Además, son árboles llenos, salvo el último nivel, que puede estar incompleto. Y cada nivel se completa de izquierda a derecha.

Existe otra propiedad, esta en lo referente al ordenamiento. Existen dos tipos de montículos binarios: de máximos y de mínimos. En los primeros se cumple que el valor de cada nodo es mayor o igual que los valores de sus nodos hijos. En los segundos, el valor de cada nodo es menor o igual que los valores de sus nodos hijos.

Dado que para cada nodo se cumple esta segundo propiedad, cada nodo se comporta como un montículo.

Resumiendo, un montículo binario debe tener las siguientes propiedades:

• Todos los niveles están completos, excepto el último, que puede no estarlo.
• Se llena por niveles, y cada nivel se llena de izquierda a derecha.
• Están ordenados, pero de arriba a abajo.

Dado el orden en que se llena el árbol, cada nodo puede numerarse. Si empezamos en 0, al primer nodo, correspondiente a la raíz, le corresponde el número 0. A sus dos hijos les corresponden los números 1 y 2, izquierda y derecha, respectivamente. A los nodos hijos del 2, le corresponden los números 3 y 4, etc.

Debido a esto, es posible crear un montículo usando directamente un array, ya que sus propiedades hacen que la posición de cada hijo se pueda calcular fácilmente en una estructura lineal. Esto tiene la ventaja de que no es necesario almacenar los punteros a los nodos hijos.

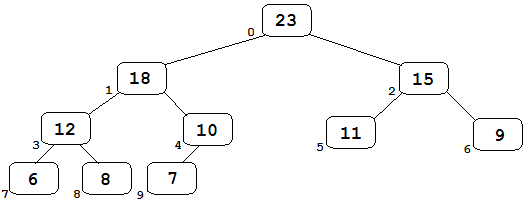
Para calcular los índices de los nodos hijos de cualquier nodo basta con multiplicar el índice del nodo padre por dos, para el hijo izquierdo, y multiplicar por dos y sumar uno para el hijo derecho: hijoIzq(i) = 2*i+1, hijoDer(i) = 2*i+2.

Para calcular el índice del nodo padre de cualquier nodo basta con tomar la parte entera de la división entre dos del índice del nodo menos uno, o sencillamente, hacer la división entera del índice menos uno entre dos: padreNodo(i) = (i-1)/2.

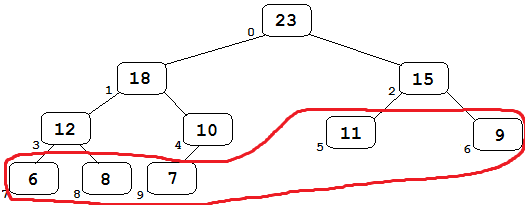
Otra propiedad interesante es que la segunda mitad de los elementos del montículo son nodos hoja, es decir, nodos sin hijos. Dado cualquier montículo con n elementos los n/2 primeros son nodos con hijos, es decir, pueden considerarse montículos, y el resto son nodos hoja. Veremos la importancia de esto cuando tengamos que convertiro un array cualquiera en un montículo.

10.2 Insertar un nodo

Dado que los montículos se llenan por niveles, insertar un valor nuevo implica hacerlo en la última posición. En general, después de insertar un valor, el montículo habrá perdido la propiedad del orden, de modo que ésta deberá ser restaurada.

Para hacer esto compararemos la clave insertada con la del nodo padre, si no se cumple la propiedad de orden, se intercambian los valores. En un montúculo de máximos, si la clave del nodo hijo es mayor que la del nodo padre, se intercambian. El proceso se repite con el nodo padre, hasta llegar al nodo raíz o hasta que no se produzca un intercambio.

A este proceso se le denomina "subir", ya que las claves suben por el árbol hasta encontrar su posición final.

10.3 Eliminar un nodo

De forma análoga, al eliminar un nodo cualquiera del árbol, para mantener el orden de llenado, lo que haremos será sustituir el valor almacenado en el nodo a borrar por el del último nodo del árbol. Esto elimina el último nodo, pero probablemente también hará que el montículo pierda su propiedad de orden.

Para restaurar el orden compararemos la clave actual del nodo sustituido con las de sus dos hijos y si es menor que alguna de ellas, la intercambiaremos con la mayor. El proceso se repite con el nodo hijo cuya clave hemos intercambiado, hasta que lleguemos a un nodo hoja, y se interrumpirá cuando no sea necesario hacer un intercambio.

En este algoritmo hay más condiciones y casos posibles. Dado que un nodo puede tener dos, uno o ningún nodo hijo.

A este proceso se le demonima "bajar", ya que las claves bajan por el árbol hasta encontrar su posición final.

10.4 Propiedades y funciones a implementar en un montículo binario

Si se usase una estructura dinámica para implementar el montículo, tendríamos que almacenar como propiedades un puntero a la raíz del árbol, y otro al último nodo insertado. La estructura de esos nodos tendrá cuatro punteros, uno lo usaremos para apuntar al siguiente nodo según el orden de llenado, y el segundo apuntará al nodo padre, esto es necesario porque no podremos usar una fórmula sencilla para calcular la posición del nodo padre. También sería necesario almacenar otros dos punteros a los nodos hijos, ya que veremos que será necesario acceder a ellos cuando se eliminen nodos. Esto hace que usar una estructura en árbol sea poco eficiente para implementar montículos.

Es más habitual usar un array para almacenar los valores del montículo. En ese caso almacenaremos el propio array y el índice del último elemento ocupado.

En cuanto a los métodos, implementaremos los siguientes:

Constructor: podemos construir el mónticulo vacío, con una capacidad máxima, o a partir de un array cuyos elementos tengan un orden arbitrario. En el caso de implementarlo en C++, se puede añadir un constructor copia.

Destructor.

Convertir: a partir de un array con los elementos desordenados, convertirlo en un montículo.

Insertar: insertar un nuevo elemento, de modo que el montículo resultante siga teniendo las propiedades de montículo.

Borrar: elimina el valor en la posición indicada.

ExtraerMaximo: devuelve el valor máximo almacenado en el montículo, y lo elimina.

Añadiremos algunas funciones auxiliares:

Subir: sube el valor de un nodo hasta que llegue a su posición final.

Bajar: baja el valor de un nodo hasta que llegue a su posición final.

Padre: calcula el valor del índice del nodo padre de un nodo dado su índice.

Izquierdo: calcula el valor del índice del nodo hijo izquierdo de un nodo dado su índice.

Derecho: calcula el valor del índice del nodo hijo derecho de un nodo dado su índice.

10.5 Algoritmos

Veamos ahora con más detalle algunos de los algoritmos usados para implementar las funciones anteriores. Para estos algoritmos asumiremos que los índices empiezan en 0, es decir, que la raíz estará almacenada en la posición 0 del array.

También asumiremos que se trata de un montículo de máximos. Los algoritmos se pueden modificar fácilmente para adapatarlos a montículos de mínimos.

10.5.1 Subir

Veremos el algoritmo definido de forma recursiva, ya que resulta más sencillo de comprender. En los programas de ejemplo implementaremos una forma iterativa, ya que resulta más eficiente.

• Subir nodo i:
• Si (i no es la raíz) y (clave[i] > clave[padre de i])
  • Intercambiar clave[i] con clave[padre de i]
  • Subir(padre de i)

10.5.2 Bajar

Al igual que con el algoritmo de "Subir", veremos la definición recursiva. En los programas de ejemplo implementaremos una forma iterativa.

• Bajar nodo i:
• Si (i < nElementos/2) No se trata de un nodo hoja, podemos bajar más.
  • maximo = i: No sabemos que nodo contiene el máximo, empezamos asumiendo que lo tiene el nodo actual.
  • Si (existe hijo_derecho(i)) y (clave[hijo_derecho(i)] > clave[i])
    • maximo = hijo_derecho(i)
  • Si (clave[hijo_izquierdo(i)] > clave[maximo])
    • maximo = hijo_izquierdo[i]
  • Si (maximo != i)
    • Intercambiar clave[i] con clave[maximo]
    • Bajar(maximo)

10.5.3 Insertar

Insertar un nuevo valor es sencillo, disponiendo de la función Subir. Asumiremos que los nodos se numeran a partir de 0. De modo que el número de elementos, nElementos es siempre una unidad mayor que el índice de la última posición ocupada. Es decir, en un montículo con n valores almacenados, el último valor estará almacenado en la posición n-1.

• Insertar(v)
• Insertar v[nElementos]: (En última posición.)
• Incrementar nElementos
• Subir(nElementos-1)

10.5.4 Borrar

Borrar el máximo equivale a eliminar el primer elemento del montículo, o más concretamente, a sustituirlo por el último, decremetar el número de elementos, y bajar la clave en la raíz a su posición final.

De forma más general, borrar un elemento cualquiera consiste en sustituir su valor por el del último elemento, decrementar el número de elementos, y bajar la clave en la posición borrada hasta su posición final.

• Borrar(i)
• Decrementar nElementos.
• clave[i] = clave[nElementos]
• Bajar(i)

10.5.5 Extraer máximo

Extraer el máximo equivale a eliminar el primer elemento del montículo, o más concretamente, a sustituirlo por el último, decremetar el número de elementos, y bajar la clave en la raíz a su posición final. Deberemos almacenar el valor máximo antes de borrarlo, para poder retornalo.

• ExtraerMaximo
• maximo = clave[0]
• Borrar(0)
• Retornar maximo

10.5.6 Convertir

Dado un array y su número de elementos, este algoritmo convierte el array en un montículo. El método es sencillo, basta con bajar cada uno de los nodos que no son hojas a su posición final, empezando por el último.

• Convertir
• i = nElementos/2: (Empezamos por el último nodo no hoja)
• Mientras (i >= 0): (Hasta llegar a la raíz)
  • Bajar(i)
  • i = i-1

10.6 Usos

Los montículos están diseñados para implementar colas con prioridad, sobre todo cuando el tiempo de ejecución es crítico, ya que los tiempos de inserción y borrado son constantes e dependen poco del número de elementos en el montículo.

También se pueden usar para ordenar arrays, de hecho, son la base del método de ordenamiento heapsort.

El algoritmo usado para crear un montículo desde un array cualquiera ilustra el funcionamiento de este algoritmo.

10.7 Codificación en C

Ejemplo de implementación de un montículo de máximos para enteros en C.

/*
 * TDA Heap C
 * Salvador Pozo Coronado
 * Febrero 2013 Con Clase
 */

#include <stdio.h>
#include <stdlib.h>

int random(int rango) {
    return (rand()*rango)/RAND_MAX;
}

typedef struct {
    int *heap;
    int capacidad;
    int iUltimo;
} Heap;

void Construir(Heap *h, int tam);
void MonticuloDesdeArray(Heap *h, int* vec, int tam);
void Destruir(Heap *h);

void Convertir(Heap h);
void Insertar(Heap *h, int v);
void Borrar(Heap *h, int i);
int ExtraerMaximo(Heap *h);
int Vacio(Heap h);
void Mostrar(Heap h);

/* Funciones auxiliares */
void Reubicar(Heap *h, int ncap);
void Intercambia(Heap h, int i1, int i2);
void Subir(Heap h, int i);
void Bajar(Heap h, int i);
int Padre(Heap h, int i);
int Izquierdo(Heap h, int i);
int Derecho(Heap h, int i);

void Construir(Heap *h, int tam){
    h->capacidad = tam;
    h->iUltimo = 0;
    h->heap = (int*)malloc(sizeof(int) * tam);
}

void MonticuloDesdeArray(Heap *h, int *vec, int tam) {
    int i;

    h->capacidad = tam;
    h->iUltimo = tam;
    h->heap = (int*)malloc(sizeof(int) * h->capacidad);
    for(i = 0; i < h->iUltimo; i++) h->heap[i] = vec[i];
    Convertir(*h);
}

void Destruir(Heap *h) {
    free(h->heap);
}

void Convertir(Heap h) {
    int i;

    for(i = h.iUltimo/2; i >= 0 ; i--) {
        Bajar(h, i);
    }
}

void Insertar(Heap *h, int v) {
    if(h->iUltimo >= h->capacidad) Reubicar(h, h->capacidad*2);

    h->heap[h->iUltimo++] = v;
    Subir(*h, h->iUltimo-1);
}

void Borrar(Heap *h, int i) {
    if(i < h->iUltimo) {
        h->heap[i] = h->heap[--h->iUltimo];
        Bajar(*h, i);
    }
}

int ExtraerMaximo(Heap *h) {
    int retval = h->heap[0];

    Borrar(h, 0);

    return retval;
}

void Reubicar(Heap *h, int ncap) {
    int *heap2;
    int i;

    heap2 = (int*)malloc(sizeof(int) * ncap);
    for(i = 0; i < h->iUltimo; i++) heap2[i] = h->heap[i];
    if(h->heap) free(h->heap);
    h->heap = heap2;
    h->capacidad = ncap;
}

void Intercambia(Heap h, int i1, int i2) {
    int aux;

    aux = h.heap[i1];
    h.heap[i1] = h.heap[i2];
    h.heap[i2] = aux;
}

// Algoritmo no recursivo para subir
void Subir(Heap h, int i) {
    int iPadre;

    while(i > 0 && h.heap[i] > h.heap[iPadre=Padre(h, i)]) {
        Intercambia(h, i, iPadre);
        i = iPadre;
    }
}

void Bajar(Heap h, int i){
    int iIzq, iDer, maximo;

    maximo = i;
    do{
        i = maximo;
        iIzq=Izquierdo(h, i);
        iDer=Derecho(h, i);
        if(iDer < h.iUltimo && h.heap[iDer] > h.heap[maximo]) maximo = iDer;
        if(iIzq < h.iUltimo && h.heap[iIzq] > h.heap[maximo]) maximo = iIzq;
        if(i != maximo) Intercambia(h, i, maximo);
    } while (i != maximo && maximo < h.iUltimo/2);
}

int Padre(Heap h, int i) {
    return (i-1)/2;
}

int Izquierdo(Heap h, int i) {
    return 2*i+1;
}

int Derecho(Heap h, int i) {
    return 2*i+2;
}

int Vacio(Heap h) {
    return h.iUltimo == 0;
}

void Mostrar(Heap h) {
    int i;

    if(Vacio(h)) printf("Heap vacio\n");
    else {
        for(i = 0; i < h.iUltimo; i++) printf("%d,", h.heap[i]);
        printf("\n");
    }
}

int main()
{
    Heap h1;
    int i;

    Construir(&h1, 10);
    for(i = 0; i < 20; i++) Insertar(&h1, random(200));

    Mostrar(h1);
    while(!Vacio(h1)) {
        printf("%d:", ExtraerMaximo(&h1));
    }
    printf("\n");
    Destruir(&h1);

    int v[] = {43, 23, 12, 4, 45, 32, 18, 6, 17};
    Heap h2;
    MonticuloDesdeArray(&h2, v, sizeof(v)/sizeof(int));
    Mostrar(h2);
    while(!Vacio(h2)) {
        printf("%d:", ExtraerMaximo(&h2));
    }
    Destruir(&h2);

    return 0;
}

10.8 Codificación en C++

Ejemplo de implementación de un montículo de máximos para enteros en C++.

/*
 * TDA Heap C++
 * Salvador Pozo Coronado
 * Febrero 2013 Con Clase
 */

#include <iostream>
#include <cstdlib>

using namespace std;

int random(int rango) {
    return (rand()*rango)/RAND_MAX;
}

class Heap {
    public:
        Heap(int tam=10);
        Heap(int *vec, int tam);
        Heap(Heap &);
        ~Heap();
        void Convertir();
        void Insertar(int v);
        void Borrar(int i);
        int ExtraerMaximo();
        bool Vacio() { return iUltimo == 0; }
        void Mostrar();
    private:
        void Reubicar(int ncap);
        void Intercambia(int i1, int i2);
        void Subir(int i);
        void Bajar(int i);
        int Padre(int i) { return (i-1)/2; }
        int Izquierdo(int i) { return 2*i+1; }
        int Derecho(int i) { return 2*i+2; }
        int *heap;
        int capacidad;
        int iUltimo;
};

Heap::Heap(int tam) : capacidad(tam), iUltimo(0) {
    heap = new int[tam];
}

Heap::Heap(int *vec, int tam) : capacidad(tam), iUltimo(tam) {
    heap = new int[capacidad];
    for(int i = 0; i < iUltimo; i++) heap[i] = vec[i];
    Convertir();
}

Heap::Heap(Heap &h) : capacidad(h.capacidad), iUltimo(h.iUltimo) {
    heap = new int[capacidad];
    for(int i = 0; i < iUltimo; i++) heap[i] = h.heap[i];
}

Heap::~Heap() {
    delete[] heap;
}

// Para cada elemento, verificar si el valor de sus hijos es menor
// Si alguno es mayor, intercambiar valor del elemento con el mayor de los hijos.
//           0
//      1          2
//   3    4     5     6
// 7  8  9 10 11 12 13 14
void Heap::Convertir() {
    for(int i = iUltimo/2; i >= 0 ; i--) {
        Bajar(i);
    }
}

void Heap::Insertar(int v) {
    if(iUltimo >= capacidad) Reubicar(capacidad*2);

    heap[iUltimo++] = v;
    Subir(iUltimo-1);
}

void Heap::Borrar(int i) {
    if(i < iUltimo) {
        heap[i] = heap[--iUltimo];
        Bajar(i);
    }
}

int Heap::ExtraerMaximo() {
    int retval = heap[0];

    Borrar(0);

    return retval;
}

void Heap::Reubicar(int ncap) {
    int *heap2;

    heap2 = new int[ncap];
    for(int i = 0; i < iUltimo; i++) heap2[i] = heap[i];
    if(heap) delete[] heap;
    heap = heap2;
    capacidad = ncap;
}

void Heap::Intercambia(int i1, int i2) {
    int aux;

    aux = heap[i1];
    heap[i1] = heap[i2];
    heap[i2] = aux;
}

// Algoritmo no recursivo para subir
void Heap::Subir(int i) {
    int iPadre;

    while(i > 0 && heap[i] > heap[iPadre=Padre(i)]) {
        Intercambia(i, iPadre);
        i = iPadre;
    }
}

void Heap::Bajar(int i){
    int iIzq, iDer, maximo;

    maximo = i;
    do{
        i = maximo;
        iIzq=Izquierdo(i);
        iDer=Derecho(i);
        if(iDer < iUltimo && heap[iDer] > heap[maximo]) maximo = iDer;
        if(iIzq < iUltimo && heap[iIzq] > heap[maximo]) maximo = iIzq;
        if(i != maximo) Intercambia(i, maximo);
    } while (i != maximo && maximo < iUltimo/2);
}

void Heap::Mostrar() {
    if(Vacio()) cout << "Heap vacio" << endl;
    else {
        for(int i = 0; i < iUltimo; i++) cout << heap[i] << ",";
        cout << endl;
    }
}

int main()
{
    Heap h1(10);

    for(int i = 0; i < 20; i++) h1.Insertar(random(200));

    h1.Mostrar();
    while(!h1.Vacio()) {
        cout << h1.ExtraerMaximo() << ":";
    }
    cout << endl;

    int v[] = {43, 23, 12, 4, 45, 32, 18, 6, 17};
    Heap h2(v, sizeof(v)/sizeof(int));
    h2.Mostrar();
    while(!h2.Vacio()) {
        cout << h2.ExtraerMaximo() << ":";
    }

    return 0;
}

10.9 Codificación en C++ con plantillas

Ejemplo de implementación de un montículo de máximos en C++ usando plantillas.

/*
 * TDA Vector C++ con Plantillas
 * Salvador Pozo Coronado
 * Febrero 2013 Con Clase
 */
 #include <iostream>

using namespace std;

template<class TIPO> class vector {
    public:
        vector(int m);
        vector(vector& v);
        ~vector();
        void Reservar(int ncap);
        void Redimensionar(int nm);
        TIPO &operator[](int n);
        void Agregar(TIPO dato);
        TIPO Sustraer();
        void Asignar(int cuenta, TIPO dato);
        TIPO &Primero();
        TIPO &Ultimo();
        void Insertar(int pos, TIPO val);
        void Eliminar(int pos);
        /* Borra todos los elementos del vector */
        void Borrar() { medida = 0; }
        /* Devuelve el número de elementos del vector */
        int Medida() { return medida; }
        /* Devuelve un valor true si el vector está vacío */
        bool Vacio() { return !medida; }
        /* Devuelve la capacidad actual del vector */
        int Capacidad() { return capacidad; }

    private:
        void Reubicar(int ncap);

        TIPO *datos;
        int medida;
        int capacidad;
};

/* Inicia el vector con una capacidad cap */
template<class TIPO>
vector<TIPO>::vector(int cap) : medida(0), capacidad(cap) {
    datos = new TIPO[cap];
}

/* Constructor copia */
template<class TIPO>
vector<TIPO>::vector(vector& v) : medida(v.medida), capacidad(v.capacidad) {
    datos = new TIPO[v.capacidad];
    for(int i = 0; i < medida; i++)
        datos[i] = v.datos[i];
}

template<class TIPO>
vector<TIPO>::~vector() {
    delete[] datos;
}

template<class TIPO>
void vector<TIPO>::Reubicar(int ncap) {
    int *datos2;
    int i;

    datos2 = new TIPO[ncap];
    for(i = 0; i < min(capacidad, ncap); i++) datos2[i] = datos[i];
    if(datos) delete[] datos;
    datos = datos2;
}

/* Aumenta la capacidad del vector a la nueva capacidad ncap */
template<class TIPO>
void vector<TIPO>::Reservar(int ncap) {
    if(ncap > capacidad) Reubicar(ncap);
    capacidad = ncap;
}

/* Aumenta la capacidad del vector para que pueda almacenar al menos nm elementos */
template<class TIPO>
void vector<TIPO>::Redimensionar(int nm) {
    int cap = capacidad;
    while(nm > cap) cap *= 2;
    Reubicar(cap);
    capacidad = cap;
}

/* Retorna un puntero al elemento n del vector */
template<class TIPO>
TIPO &vector<TIPO>::operator[](int n) {
    return datos[n];
}

/* Añade un elemento de valor d al final del vector */
template<class TIPO>
void vector<TIPO>::Agregar(TIPO d) {
    if(medida == capacidad) Redimensionar(medida+1);

    datos[medida++] = d;
}

/* Elimina el último elemento del vector, y devuelve su valor */
template<class TIPO>
TIPO vector<TIPO>::Sustraer() {
    if(medida > 0) return datos[--medida];
    else return 0;
}

/* Asigna el valor dato a los primeros cuenta elementos del vector */
template<class TIPO>
void vector<TIPO>::Asignar(int cuenta, TIPO dato) {
    for(int i = 0; i < cuenta; i++) Agregar(dato);
}

/* Devuelve el valor del primer elemento del vector */
template<class TIPO>
TIPO &vector<TIPO>::Primero() {
    if(medida > 0) return datos[0];
    else return datos[0];
}

/* Devuelve el valor del último elemento del vector */
template<class TIPO>
TIPO &vector<TIPO>::Ultimo() {
    if(medida > 0) return datos[medida-1];
    else return datos[0];
}

/* Inserta el valor val en la posición pos del vector */
template<class TIPO>
void vector<TIPO>::Insertar(int pos, TIPO val) {
    if(medida == capacidad) Redimensionar(medida+1);
    for(int i = medida; i > pos; i--) datos[i] = datos[i-1];
    datos[pos] = val;
    medida++;
}

/* Elimina el valor de la posición pos del vector */
template<class TIPO>
void vector<TIPO>::Eliminar(int pos) {
    if(pos < medida) {
        for(int i = pos; i < medida-1; i++) datos[i] = datos[i+1];
        medida--;
    }
}

int main() {
    vector<int> v(10);
    int i;

    v.Asignar(10, 0);

    for(i = 0; i < 10; i++) v[i] = i;
    for(i = 0; i < 10; i++) v.Agregar(100+i);
    vector<int> v2(v);
    v.Agregar(23);

    v.Insertar(15, 1000);
    v.Eliminar(16);
    v.Eliminar(108);

    for(i = 0; i < v.Medida(); i++)
        cout << "v[" << i << "] = " << v[i] << endl;
    v[3] = 30;
    cout << "v[3] = " << v[3] << endl;

    cout << "Primero = " << v.Primero() << endl;
    cout << "Ultimo = " << v.Ultimo() << endl;

    cout << "v[ultimo] = " << v.Sustraer() << endl;
    cout << "v[ultimo] = " << v.Sustraer() << endl;


    for(i = 0; i < v2.Medida(); i++)
        cout << "v2[" << i << "] = " << v2[i] << endl;
    return 0;
}